
【题目】函数![]() 中,
中,![]() 满足对
满足对![]() 有
有![]() ,当
,当![]() 时,
时,![]() ;函数
;函数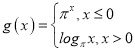 ;函数
;函数![]() .现给出
.现给出![]() 是偶函数;
是偶函数;![]() 在
在![]() 上单调递增;
上单调递增;![]() 无最大值;
无最大值;![]() 有
有![]() 个零点这四个结论,则正确结论的编号是( )
个零点这四个结论,则正确结论的编号是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
由条件![]() 满足对
满足对![]() 有
有![]() ,
,![]() 时,
时,![]() ,
,
可得函数![]() 的图像特点,再结合
的图像特点,再结合![]() 的表达式,对4个命题进行逐一判断,即可找出正确的命题,得到答案.
的表达式,对4个命题进行逐一判断,即可找出正确的命题,得到答案.
![]() 满足对
满足对![]() 有
有![]() ,
,![]() 时,
时,![]()
将![]() 在
在![]() 上的图像向右平移个
上的图像向右平移个![]() 单位,再将纵坐标扩到为原来的2倍,得到
单位,再将纵坐标扩到为原来的2倍,得到![]() 上的图像.
上的图像.
将![]() 在
在![]() 上的图像向右平移个
上的图像向右平移个![]() 单位,再将纵坐标扩到为原来的2倍,得到
单位,再将纵坐标扩到为原来的2倍,得到![]() 上的图像.
上的图像.
将![]() 在
在![]() 上的图像向左平移个
上的图像向左平移个![]() 单位,再将纵坐标变为为原来的
单位,再将纵坐标变为为原来的![]() ,得到
,得到![]() 上的图像,
上的图像,
依此类推可得![]() 的图像,如图.
的图像,如图.
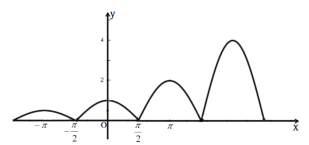
所以![]() 不是周期函数,所以
不是周期函数,所以![]() 错误.
错误.
由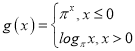 ,作出其函数图像,如图.
,作出其函数图像,如图.
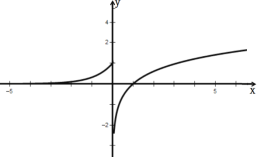
由图显然![]() 在
在![]() 上不是单调递增函数,所以
上不是单调递增函数,所以![]() 错误.
错误.
当![]() 大于0,且
大于0,且![]() 时,
时,![]() .
.
所以当![]() 大于0,且
大于0,且![]() 时
时![]() .
.
所以![]() 无最大值,故
无最大值,故![]() 正确.
正确.
函数![]() 的零点个数,即函数
的零点个数,即函数![]() 与
与![]() 图像的在
图像的在![]() 上交点的个数.
上交点的个数.
作出函数![]() 与
与![]() 的图像,如同
的图像,如同
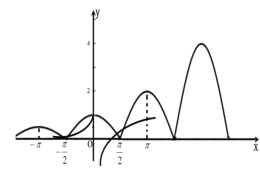
由图像可知, 函数![]() 与
与![]() 图像的在
图像的在![]() 上有5个交点,故
上有5个交点,故![]() 正确.
正确.
故选: D


科目:高中数学 来源: 题型:
【题目】电影《厉害了,我的国》于2018年3月正式登陆全国院线,网友纷纷表示,看完电影热血沸腾“我为我的国家骄傲,我为我是中国人骄傲!”《厉害了,我的国》正在召唤我们每一个人,不忘初心,用奋斗书写无悔人生,小明想约甲、乙、丙、丁四位好朋友一同去看《厉害了,我的国》,并把标识为![]() 的四张电影票放在编号分别为1,2,3,4的四个不同的盒子里,让四位好朋友进行猜测:
的四张电影票放在编号分别为1,2,3,4的四个不同的盒子里,让四位好朋友进行猜测:
甲说:第1个盒子里放的是![]() ,第3个盒子里放的是
,第3个盒子里放的是![]()
乙说:第2个盒子里放的是![]() ,第3个盒子里放的是
,第3个盒子里放的是![]()
丙说:第4个盒子里放的是![]() ,第2个盒子里放的是
,第2个盒子里放的是![]()
丁说:第4个盒子里放的是![]() ,第3个盒子里放的是
,第3个盒子里放的是![]()
小明说:“四位朋友你们都只说对了一半”
可以预测,第4个盒子里放的电影票为_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放以来,中国快递行业持续快速发展,快递业务量从上世纪![]() 年代的
年代的![]() 万件提升到2018年的
万件提升到2018年的![]() 亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于
亿件,快递行业的发展也给我们的生活带来了很大便利.已知某市某快递点的收费标准为:首重(重量小于等于![]() )收费
)收费![]() 元,续重
元,续重![]() 元
元![]() (不足
(不足![]() 按
按![]() 算). (如:一个包裹重量为
算). (如:一个包裹重量为![]() 则需支付首付
则需支付首付![]() 元,续重
元,续重![]() 元,一共
元,一共![]() 元快递费用)
元快递费用)
(1)若你有三件礼物![]() 重量分别为
重量分别为![]() ,要将三个礼物分成两个包裹寄出(如:
,要将三个礼物分成两个包裹寄出(如:![]() 合为一个包裹,
合为一个包裹,![]() 一个包裹),那么如何分配礼物,使得你花费的快递费最少?
一个包裹),那么如何分配礼物,使得你花费的快递费最少?
(2)为了解该快递点2019年的揽件情况,在2019年内随机抽查了![]() 天的日揽收包裹数(单位:件),得到如下表格:
天的日揽收包裹数(单位:件),得到如下表格:
包裹数(单位:件) |
|
|
|
|
天数(天) |
|
|
|
|
现用这![]() 天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取
天的日揽收包裹数估计该快递点2019年的日揽收包裏数.若从2019年任取![]() 天,记这
天,记这![]() 天中日揽收包裹数超过
天中日揽收包裹数超过![]() 件的天数为随机变量
件的天数为随机变量![]() 求
求![]() 的分布列和期望
的分布列和期望
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线
轴的正半轴为极轴,且与直角坐标系长度单位相同的极坐标系中,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() .若直
.若直![]() 与曲线
与曲线![]() 相交于两点
相交于两点![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国于2015年10月宣布实施普遍二孩政策,为了解户籍、性别对生育二胎选择倾向的影响,某地从育龄群体中随机抽取了容量为140的调查样本,其中城镇户籍与农村户籍各70人;男性60人,女性80人,绘制的不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图如图所示,其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述正确的是( )
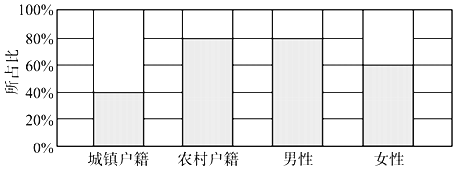
A.是否倾向选择生育二胎与户籍有关
B.是否倾向选择生育二胎与性别有关
C.调查样本中倾向选择生育二胎的群群中,男性人数与女性人数相同
D.倾向选择不生育二胎的群群中,农村户籍人数多于城镇户籍人数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会于2019年10月18日至27日在中国武汉举行,中国队以133金64银42铜位居金牌榜和奖牌榜的首位.运动会期间有甲、乙等五名志愿者被分配到射击、田径、篮球、游泳四个运动场地提供服务,要求每个人都要被派出去提供服务,且每个场地都要有志愿者服务,则甲和乙恰好在同一组的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为考察某动物疫苗预防某种疾病的效果,现对200只动物进行调研,并得到如下数据:
未发病 | 发病 | 合计 | |
未注射疫苗 | 20 | 60 | 80 |
注射疫苗 | 80 | 40 | 120 |
合计 | 100 | 100 | 200 |
(附: )
)
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
则下列说法正确的:( )
A.至少有99.9%的把握认为“发病与没接种疫苗有关”
B.至多有99%的把握认为“发病与没接种疫苗有关”
C.至多有99.9%的把握认为“发病与没接种疫苗有关”
D.“发病与没接种疫苗有关”的错误率至少有0.01%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com