
【题目】给定椭圆![]() :
:![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆
的圆是椭圆![]() 的“伴椭圆”,若椭圆
的“伴椭圆”,若椭圆![]() 的一个焦点为
的一个焦点为![]() ,其短轴上一个端点到
,其短轴上一个端点到![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)过点![]() 作椭圆
作椭圆![]() 的“伴随圆”
的“伴随圆”![]() 的动弦
的动弦![]() ,过点
,过点![]() 、
、![]() 分别作“伴随圆”
分别作“伴随圆”![]() 的切线,设两切线交于点
的切线,设两切线交于点![]() ,证明:点
,证明:点![]() 的轨迹是直线,并写出该直线的方程;
的轨迹是直线,并写出该直线的方程;
(3)设点![]() 是椭圆
是椭圆![]() 的“伴随圆”
的“伴随圆”![]() 上的一个动点,过点
上的一个动点,过点![]() 作椭圆
作椭圆![]() 的切线
的切线![]() 、
、![]() ,试判断直线
,试判断直线![]() 、
、![]() 是否垂直?并说明理由.
是否垂直?并说明理由.
【答案】(1)![]() ;
;
(2)见解析;
(3)见解析.
【解析】
(1)由题意可得,![]() ,则
,则![]() ,从而得到椭圆C的方程;
,从而得到椭圆C的方程;
(2)根据题意,求得![]() ,分直线的斜率存在与不存在两种情况,将斜率存在时求得的直线,对斜率不存在时求得的点P的坐标进行检验,最后求得结果.
,分直线的斜率存在与不存在两种情况,将斜率存在时求得的直线,对斜率不存在时求得的点P的坐标进行检验,最后求得结果.
(3)讨论当P在直线![]() 上时,设出直线方程,联立椭圆方程,消去
上时,设出直线方程,联立椭圆方程,消去![]() ,得到关于
,得到关于![]() 的方程,运用判别式为0,化简整理,得到关于
的方程,运用判别式为0,化简整理,得到关于![]() 的方程,求出连根之积,判断是否为
的方程,求出连根之积,判断是否为![]() ,即可判断
,即可判断![]() 垂直.
垂直.
(1)依题意得:![]() ,所以
,所以![]() ,
,
所以椭圆方程为:![]() ;
;
(2)由题意可得伴随圆的方程为![]() ,
,
点![]() 为
为![]() ,所以
,所以![]() ,
,
当过点P的直线斜率不存在时,则![]() ,
,
可求得![]() ,此时
,此时![]() ,
,
当过点P的直线斜率存在时,设直线方程为:![]() ,
,
设![]() ,
,![]() ,
,
则经过各自的切线方程为: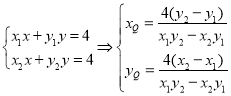 ,
,
把 代入,解得
代入,解得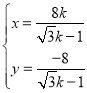 ,
,
消![]() ,得到
,得到![]() ,
,
当![]() 不存在时,
不存在时,![]() 也满足方程
也满足方程![]() ,
,
所以点![]() 的轨迹是一条直线,且方程为
的轨迹是一条直线,且方程为![]() ;
;
(3)当![]() 中有一条无斜率时,不妨设
中有一条无斜率时,不妨设![]() 无斜率,
无斜率,
因为![]() 与椭圆只有一个公共点,则其方程为:
与椭圆只有一个公共点,则其方程为:![]() ,此时经过点
,此时经过点![]() 或
或![]() ,
,
则直线![]() 的方程为:
的方程为:![]() ,经检验,满足垂直关系;
,经检验,满足垂直关系;
当![]() 斜率都存在时,设点
斜率都存在时,设点![]() ,
,
因为点P在伴随圆上,所以有![]() ,
,
设经过点![]() ,且与椭圆只有一个公共点的直线方程为:
,且与椭圆只有一个公共点的直线方程为:![]() ,
,
联立椭圆方程,
 ,消
,消![]() 化简得
化简得![]() ,
,
因为相切,所以![]() ,即:
,即:![]() ,
,
又因为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以直线![]() ,
,
从而得证.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案科目:高中数学 来源: 题型:
【题目】一对夫妇为了给他们的独生孩子支付将来上大学的费用,从孩子一周岁生日开始,每年到银行储蓄![]() 元一年定期,若年利率为
元一年定期,若年利率为![]() 保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为
保持不变,且每年到期时存款(含利息)自动转为新的一年定期,当孩子18岁生日时不再存入,将所有存款(含利息)全部取回,则取回的钱的总数为![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
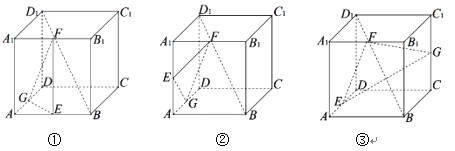
【题目】如图,在下列三个正方体![]() 中,
中,![]() 均为所在棱的中点,过
均为所在棱的中点,过![]() 作正方体的截面.在各正方体中,直线
作正方体的截面.在各正方体中,直线![]() 与平面
与平面![]() 的位置关系描述正确的是
的位置关系描述正确的是
A. ![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②③
的有且只有②③
B. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有①
的有且只有①
C. .![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②
的有且只有②
D. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有③
的有且只有③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=2,前3项和为S3=![]() .
.
(1)求{an}的通项公式;
(2)设等比数列{bn}满足b1=a1,b4=a15,求{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
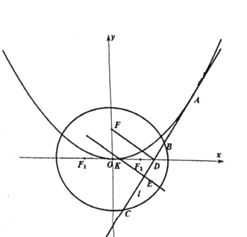
【题目】已知抛物线![]() ,
,![]() 为其焦点,椭圆
为其焦点,椭圆![]() ,
,![]() ,
,![]() 为其左右焦点,离心率
为其左右焦点,离心率![]() ,过
,过![]() 作
作![]() 轴的平行线交椭圆于
轴的平行线交椭圆于![]() 两点,
两点,![]() .
.
(1)求椭圆的标准方程;
(2)过抛物线上一点![]() 作切线
作切线![]() 交椭圆于
交椭圆于![]() 两点,设
两点,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,![]() 的中点为
的中点为![]() ,
,![]() 的中垂线交
的中垂线交![]() 轴为
轴为![]() ,
,![]() ,
,![]() 的面积分别记为
的面积分别记为![]() ,
,![]() ,若
,若![]() ,且点
,且点![]() 在第一象限.求点
在第一象限.求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地的中小学办学条件在政府的教育督导下,迅速得到改变.教育督导一年后.分别随机抽查了初中(用![]() 表示)与小学(用
表示)与小学(用![]() 表示)各10所学校.得到相关指标的综合评价得分(百分制)的茎叶图如图所示.则从茎叶图可得出正确的信息为( )(80分及以上为优秀). ①初中得分与小学得分的优秀率相同;②初中得分与小学得分的中位数相同③初中得分的方差比小学得分的方差大④初中得分与小学得分的平均分相同.
表示)各10所学校.得到相关指标的综合评价得分(百分制)的茎叶图如图所示.则从茎叶图可得出正确的信息为( )(80分及以上为优秀). ①初中得分与小学得分的优秀率相同;②初中得分与小学得分的中位数相同③初中得分的方差比小学得分的方差大④初中得分与小学得分的平均分相同.

A.①②B.①③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国铁路总公司相关负责人表示,到2018年底,全国铁路营业里程达到13.1万公里,其中高铁营业里程2.9万公里,超过世界高铁总里程的三分之二,下图是2014年到2018年铁路和高铁运营里程(单位:万公里)的折线图,以下结论不正确的是( )

A.每相邻两年相比较,2014年到2015年铁路运营里程增加最显著
B.从2014年到2018年这5年,高铁运营里程与年价正相关
C.2018年高铁运营里程比2014年高铁运营里程增长80%以上
D.从2014年到2018年这5年,高铁运营里程数依次成等差数列
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com