
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,判断函数
时,判断函数![]() 的零点个数;
的零点个数;
(Ⅱ)若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)函数![]() 的零点个数为1;(Ⅱ)
的零点个数为1;(Ⅱ)![]()
【解析】
(Ⅰ)根据题意,代入![]() ,对函数求导,判断函数单调性,根据特殊值
,对函数求导,判断函数单调性,根据特殊值![]() ,即可判断零点个数;
,即可判断零点个数;
(Ⅱ)根据题意,解决函数![]() 恒成立问题,方法一:转化
恒成立问题,方法一:转化![]() 对任意
对任意![]() 恒成立,则有
恒成立,则有![]() 对任意
对任意![]() 恒成立,构造函数
恒成立,构造函数![]() ,只需求
,只需求![]() ,利用导数研究函数最值问题。方法二:
,利用导数研究函数最值问题。方法二:![]() 对任意
对任意![]() 恒成立.构造函数
恒成立.构造函数![]() ,转化成射线
,转化成射线![]() 与函数
与函数![]() 的图象相切时属临界状态,计算求解;方法三:含参的函数最小值探究,只需
的图象相切时属临界状态,计算求解;方法三:含参的函数最小值探究,只需![]() ,即可求解参数取值范围.
,即可求解参数取值范围.
(Ⅰ)当![]() 时,
时,![]() ,其定义域为
,其定义域为![]() ,
,
求导得![]() ,
,
于是当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,又
单调递增,又![]() ,所以函数
,所以函数![]() 的零点个数为1;
的零点个数为1;
(Ⅱ)法1:因对任意![]() ,
,![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立,于是
恒成立,于是![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]() ,只需
,只需![]() .
.
对函数![]() 求导,得
求导,得![]() ,令
,令![]() ,
,
则![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,所以当
,所以当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,
,![]() ,函数
,函数![]() 单调递增,所以函数
单调递增,所以函数![]() ,于是
,于是![]() ,即实数
,即实数![]() 的取值范围为
的取值范围为![]() .
.
法2:因对任意![]() ,
,![]() 恒成立,即
恒成立,即![]() 对任意
对任意![]() 恒成立.构造函数
恒成立.构造函数![]() ,对其求导,得
,对其求导,得![]() ,
,
令![]() ,得
,得![]() (
(![]() 舍去),所以当
舍去),所以当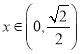 时,
时,![]() ,函数
,函数![]() 单调递减;当
单调递减;当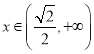 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
函数![]() 的图象是一条过原点的射线(不包括端点),旋转射线(不含端点),发现
的图象是一条过原点的射线(不包括端点),旋转射线(不含端点),发现![]() 与函数
与函数![]() 的图象相切时属临界状态.
的图象相切时属临界状态.
设切点为![]() ,则
,则![]() ,整理得
,整理得![]() ,
,
显然![]() 在
在![]() 上是增函数,又
上是增函数,又![]() ,所以
,所以![]() ,此时切线斜率为1,结合图象,可知实数
,此时切线斜率为1,结合图象,可知实数![]() 的取值范围为
的取值范围为![]() .
.
法3:根据题意只需![]() 即可.
即可.
又![]() ,令
,令![]() ,因2与
,因2与![]() 异号,所以必有一正根,不妨设为
异号,所以必有一正根,不妨设为![]() ,则
,则![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;当
单调递减;当![]() 时,
时,![]() ,函数
,函数![]() 单调递增,所以
单调递增,所以![]() ,
,
又![]() 在
在![]() 上是减函数,又
上是减函数,又![]() ,所以
,所以![]() ,
,
由![]() 得
得![]() 在
在![]() 上单调递增,则实数
上单调递增,则实数![]() 的取值范围为
的取值范围为![]() .
.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:
【题目】2019年末,武汉出现新型冠状病毒(![]() 肺炎疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,目前没有特异治疗方法.防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,某社区将本社区的排查工作人员分为
肺炎疫情,并快速席卷我国其他地区,传播速度很快.因这种病毒是以前从未在人体中发现的冠状病毒新毒株,目前没有特异治疗方法.防控难度很大.武汉市出现疫情最早,感染人员最多,防控压力最大,武汉市从2月7日起举全市之力入户上门排查确诊的新冠肺炎患者、疑似的新冠肺炎患者、无法明确排除新冠肺炎的发热患者和确诊患者的密切接触者等“四类”人员,强化网格化管理,不落一户、不漏一人.在排查期间,某社区将本社区的排查工作人员分为![]() ,
,![]() 两个小组,排查工作期间社区随机抽取了100户已排查户,进行了对排查工作态度是否满意的电话调查,根据调查结果统计后,得到如下
两个小组,排查工作期间社区随机抽取了100户已排查户,进行了对排查工作态度是否满意的电话调查,根据调查结果统计后,得到如下![]() 的列联表.
的列联表.
是否满意 组别 | 不满意 | 满意 | 合计 |
| 16 | 34 | 50 |
| 2 | 45 | 50 |
合计 | 21 | 79 | 100 |
(1)分别估计社区居民对![]() 组、
组、![]() 组两个排查组的工作态度满意的概率;
组两个排查组的工作态度满意的概率;
(2)根据列联表的数据,能否有![]() 的把握认为“对社区排查工作态度满意”与“排查工作组别”有关?
的把握认为“对社区排查工作态度满意”与“排查工作组别”有关?
附表:
|
|
|
|
|
|
|
|
|
|
|
|
附: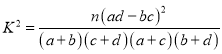
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体ABCD﹣A1B1C1D1中,点E,F分别为棱BC,CC1的中点,过点A,E,F作平面截正方体的表面所得图形是( )
A.三角形B.平行四边形C.等腰梯形D.平面五边形
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥平面ABCD,PD=2,DC=BC=1,AB=2,AB∥DC,∠BCD=90°.
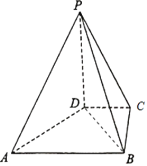
(1)求证:AD⊥PB;
(2)求A点到平面BPC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为等差数列,各项为正的等比数列
为等差数列,各项为正的等比数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,
,![]() ,__________.在①
,__________.在①![]() ;②
;②![]() ;③
;③![]() 这三个条件中任选其中一个,补充在横线上,并完成下面问题的解答(如果选择多个条件解答,则以选择第一个解答记分).
这三个条件中任选其中一个,补充在横线上,并完成下面问题的解答(如果选择多个条件解答,则以选择第一个解答记分).
(1)求数列![]() 和
和![]() 的通项公式;
的通项公式;
(2)求数列![]() 的前
的前![]() 项和
项和![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com