
| A. | (0,1) | B. | (-1,0) | C. | (-∞,-1) | D. | (-∞,-1] |
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是一个三棱锥的三视图,其俯视图是正三角形,主视图与左视图都是直角三角形.则这个三棱锥的外接球的表面积是( )
如图是一个三棱锥的三视图,其俯视图是正三角形,主视图与左视图都是直角三角形.则这个三棱锥的外接球的表面积是( )| A. | 19π | B. | 28π | C. | 67π | D. | 76π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
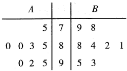 有A,B,C,D,E五位同学参加英语口语竞赛培训,现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据,这两组数据的样本茎叶图如图所示.
有A,B,C,D,E五位同学参加英语口语竞赛培训,现分别从A,B二人在培训期间参加的若干次预赛成绩中随机抽取8次得到的两组数据,这两组数据的样本茎叶图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y | 11 | 10 | 8 | 6 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com