【题目】已知△ABC的三个内角A，B，C的对边分别为a，b，c，且a，b，c成等比数列
（1）若sinC=2sinA，求cosB的值；
（2）求角B的最大值．并判断此时△ABC的形状．
【答案】
（1）解：sinC=2sinA利用正弦定理化简得：c=2a，
∵a，b，c成等比数列，∴b2=ac=2a2，即b= 
a，
∴cosB= 
= 
= 
；
（2）解：∵b2=ac，
∴cosB= = 
≥ 
= 
，
∵函数y=cosx在区间[0，π]上为减函数，
∴B∈（0， 
]，即角B的最大值为 ，
此时有a=c，且b2=ac，可得a=b=c，
则△ABC为等边三角形．
【解析】（1）利用正弦定理化简已知等式，得到c=2a，再有a，b，c成等比数列，利用等比数列的性质列出关系式，利用余弦定理表示出cosB，将得出的关系式代入计算即可求出值；（2）由表示出的cosB，将b2=ac代入利用基本不等式变形求出cosB的最小值，由余弦函数在[0，π]上为减函数，确定出B的最大值，由此时a=c及b2=ac，得出三角形ABC为等边三角形．
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识，掌握正弦定理:
．
教材全解字词句篇系列答案科目：高中数学 来源： 题型：
【题目】国际油价在某一时间内呈现出正弦波动规律：P=Asin（ωπt+ 
）+60（美元）[t（天），A＞0，ω＞0]，现采集到下列信息：最高油价80美元，当t=150（天）时达到最低油价，则ω= ．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列四组函数，表示同一函数的是（ ）
A.f（x）= 
，g（x）=x
B.f（x）=x，g（x）= 
C.f（x）=lnx2 ， g（x）=2lnx
D.f（x）=logaax（a＞0，a≠1），g（x）= 
查看答案和解析>>
科目：高中数学 来源： 题型：
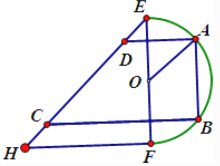
【题目】为了制作广告牌，需在如图所示的铁片上切割出一个直角梯形，已知铁片由两部分组成，半径为1的半圆
及等腰直角三角形
，其中
，为裁剪出面积尽可能大的梯形铁片
（不计损耗），将点
放在弧
上，点
放在斜边
上，且
，设
.
（1）求梯形铁片
的面积
关于
的函数关系式；
（2）试确定
的值，使得梯形铁片
的面积
最大，并求出最大值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（n）=n2cos（nπ），且an=f（n）+f（n+1），则a1+a2+a3+…+a100=（ ）
A.0
B.﹣100
C.100
D.10200
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列四组函数，表示同一函数的是（ ）
A.f（x）= 
，g（x）=x
B.f（x）=x，g（x）= 
C.f（x）=lnx2 ， g（x）=2lnx
D.f（x）=logaax（a＞0，a≠1），g（x）= 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝2cosxcos
－
sin2x＋sinxcosx.
(1)求f(x)的最小正周期；
(2)若关于x的方程
在x∈
上有两个不同的实根，求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
