
【题目】下图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.
(单位:亿元)的折线图.

为了预测该地区2018年的环境基础设施投资额,建立了![]() 与时间变量
与时间变量![]() 的两个线性回归模型.根据2000年至2016年的数据(时间变量
的两个线性回归模型.根据2000年至2016年的数据(时间变量![]() 的值依次为
的值依次为![]() )建立模型①:
)建立模型①:![]() ;根据2010年至2016年的数据(时间变量
;根据2010年至2016年的数据(时间变量![]() 的值依次为
的值依次为![]() )建立模型②:
)建立模型②:![]() .
.
(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
【答案】(1)利用模型①预测值为226.1,利用模型②预测值为256.5,(2)利用模型②得到的预测值更可靠.
【解析】分析:(1)两个回归直线方程中无参数,所以分别求自变量为2018时所对应的函数值,就得结果,(2)根据折线图知2000到2009,与2010到2016是两个有明显区别的直线,且2010到2016的增幅明显高于2000到2009,也高于模型1的增幅,因此所以用模型2更能较好得到2018的预测.
详解:(1)利用模型①,该地区2018年的环境基础设施投资额的预测值为
![]() =–30.4+13.5×19=226.1(亿元).
=–30.4+13.5×19=226.1(亿元).
利用模型②,该地区2018年的环境基础设施投资额的预测值为
![]() =99+17.5×9=256.5(亿元).
=99+17.5×9=256.5(亿元).
(2)利用模型②得到的预测值更可靠.
理由如下:
(i)从折线图可以看出,2000年至2016年的数据对应的点没有随机散布在直线y=–30.4+13.5t上下,这说明利用2000年至2016年的数据建立的线性模型①不能很好地描述环境基础设施投资额的变化趋势.2010年相对2009年的环境基础设施投资额有明显增加,2010年至2016年的数据对应的点位于一条直线的附近,这说明从2010年开始环境基础设施投资额的变化规律呈线性增长趋势,利用2010年至2016年的数据建立的线性模型![]() =99+17.5t可以较好地描述2010年以后的环境基础设施投资额的变化趋势,因此利用模型②得到的预测值更可靠.
=99+17.5t可以较好地描述2010年以后的环境基础设施投资额的变化趋势,因此利用模型②得到的预测值更可靠.
(ii)从计算结果看,相对于2016年的环境基础设施投资额220亿元,由模型①得到的预测值226.1亿元的增幅明显偏低,而利用模型②得到的预测值的增幅比较合理,说明利用模型②得到的预测值更可靠.
以上给出了2种理由,考生答出其中任意一种或其他合理理由均可得分.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】近年来,随着互联网的发展,诸如“滴滴打车”“神州专车”等网约车服务在我国各城市迅猛发展,为人们出行提供了便利,但也给城市交通管理带来了一些困难.为掌握网约车在![]() 省的发展情况,
省的发展情况,![]() 省某调查机构从该省抽取了5个城市,分别收集和分析了网约车的
省某调查机构从该省抽取了5个城市,分别收集和分析了网约车的![]() ,
,![]() 两项指标数
两项指标数![]() ,数据如下表所示:
,数据如下表所示:
城市1 | 城市2 | 城市3 | 城市4 | 城市5 | |
| 2 | 4 | 5 | 6 | 8 |
| 3 | 4 | 4 | 4 | 5 |
经计算得: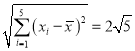 ,
,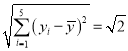 ,
,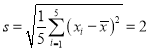 .
.
(1)试求![]() 与
与![]() 间的相关系数
间的相关系数![]() ,并利用
,并利用![]() 说明
说明![]() 与
与![]() 是否具有较强的线性相关关系(若
是否具有较强的线性相关关系(若![]() ,则线性相关程度很高,可用线性回归模型拟合);
,则线性相关程度很高,可用线性回归模型拟合);
(2)建立![]() 关于
关于![]() 的回归方程,并预测当
的回归方程,并预测当![]() 指标数为7时,
指标数为7时,![]() 指标数的估计值;
指标数的估计值;
(3)若城市的网约车![]() 指标数
指标数![]() 落在区间
落在区间![]() 之外,则认为该城市网约车数量过多,会对城市交通管理带来较大的影响,交通管理部门将介入进行治理,直至
之外,则认为该城市网约车数量过多,会对城市交通管理带来较大的影响,交通管理部门将介入进行治理,直至![]() 指标数
指标数![]() 回落到区间
回落到区间![]() 之内.现已知2018年11月该城市网约车的
之内.现已知2018年11月该城市网约车的![]() 指标数为13,问:该城市的交通管理部门是否要介入进行治理?试说明理由.
指标数为13,问:该城市的交通管理部门是否要介入进行治理?试说明理由.
附:相关公式: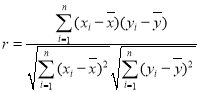 ,
,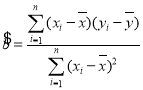 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,圆
,圆![]() 经过椭圆
经过椭圆![]() 的两个焦点和两个顶点,点
的两个焦点和两个顶点,点![]() 在椭圆
在椭圆![]() 上,且
上,且![]() ,
,![]() .
.
(Ⅰ)求椭圆![]() 的方程和点
的方程和点![]() 的坐标;
的坐标;
(Ⅱ)过点![]() 的直线
的直线![]() 与圆
与圆![]() 相交于
相交于![]() 、
、![]() 两点,过点
两点,过点![]() 与
与![]() 垂直的直线
垂直的直线![]() 与椭圆
与椭圆![]() 相交于另一点
相交于另一点![]() ,求
,求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下:
上年度出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
保费 | 0.85a | a | 1.25a | 1.5a | 1.75a | 2a |
随机调查了该险种的200名续保人在一年内的出险情况,得到如下统计表:
出险次数 | 0 | 1 | 2 | 3 | 4 | ≥5 |
频数 | 60 | 50 | 30 | 30 | 20 | 10 |
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求P(A)的估计值;
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”,求P(B)的估计值;
(3)求续保人本年度平均保费的估计值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国式过马路”存在很大的交通安全隐患.某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如下列联表:
项目 | 男性 | 女性 | 总计 |
反感 | 10 | ||
不反感 | 8 | ||
总计 | 30 |
已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是![]() .
.
(1)请将上面的列联表补充完整(直接写结果,不需要写求解过程),并据此资料分析反感“中国式过马路”与性别是否有关?
(2)若从这30人中的女性路人中随机抽取2人参加一活动,记反感“中国式过马路”的人数为X,求X的分布列和数学期望.
附:K2=![]()
.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年,国家逐步推行全新的高考制度.新高考不再分文理科,某省采用3+3模式,其中语文、数学、外语三科为必考科目,满分各150分,另外考生还要依据想考取的高校及专业的要求,结合自己的兴趣爱好等因素,在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试(6选3),每科目满分100分.为了应对新高考,某高中从高一年级1000名学生(其中男生550人,女生450人)中,采用分层抽样的方法从中抽取![]() 名学生进行调查.
名学生进行调查.
(1)已知抽取的![]() 名学生中含男生55人,求
名学生中含男生55人,求![]() 的值;
的值;
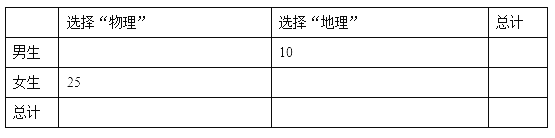
(2)学校计划在高一上学期开设选修中的“物理”和“地理”两个科目,为了了解学生对这两个科目的选课情况,对在(1)的条件下抽取到的![]() 名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的
名学生进行问卷调查(假定每名学生在这两个科目中必须选择一个科目且只能选择一个科目),下表是根据调查结果得到的![]() 列联表. 请将列联表补充完整,并判断是否有 99%的把握认为选择科目与性别有关?说明你的理由;
列联表. 请将列联表补充完整,并判断是否有 99%的把握认为选择科目与性别有关?说明你的理由;
(3)在抽取到的女生中按(2)中的选课情况进行分层抽样,从中抽出9名女生,再从这9名女生中抽取4人,设这4人中选择“地理”的人数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
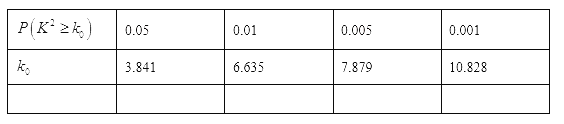
附:![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数![]() 在定义域内存在区间[a,b],使
在定义域内存在区间[a,b],使![]() 在[a,b]上的值域是[2a,2b],那么称
在[a,b]上的值域是[2a,2b],那么称![]() 为“倍增函数”。
为“倍增函数”。
(I)判断![]() =
=![]() 是否为“倍增函数”,并说明理由;
是否为“倍增函数”,并说明理由;
(II)证明:函数![]() =
=![]() 是“倍增函数”;
是“倍增函数”;
(III)若函数![]() =ln(
=ln(![]() )是“倍增函数”,写出实数m的取值范围。(只需写出结论)
)是“倍增函数”,写出实数m的取值范围。(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知斜率为1的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且线段
两点,且线段![]() 的中点为
的中点为![]() ,椭圆
,椭圆![]() 的上顶点为
的上顶点为![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,若直线
两点,若直线![]() 与
与![]() 的斜率之和为2,证明:
的斜率之和为2,证明:![]() 过定点.
过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com