
分析 由已知利用特殊角的三角函数值,两角差的余弦函数公式化简可得cosα+sinα=$\frac{1}{5}$,进而利用同角三角函数基本关系式即可计算得解.
解答 解:∵α∈($\frac{π}{2}$,π)且cos($\frac{π}{4}$-α)=$\frac{\sqrt{2}}{10}$,
∴可得:$\frac{\sqrt{2}}{2}$(cosα+sinα)=$\frac{\sqrt{2}}{10}$,解得:cosα+sinα=$\frac{1}{5}$,
∴cosα=$\frac{1}{5}$-sinα<0,sinα=$\frac{1}{5}$-cosα>0,
又∵cos2α+sin2α=1,
∴cos2α+($\frac{1}{5}$-cosα)2=1,整理可得:50cos2α-10cosα-24=0,
∴解得:cosα=-$\frac{3}{5}$,或$\frac{4}{5}$(舍去).
故答案为:-$\frac{3}{5}$.
点评 本题主要考查了特殊角的三角函数值,两角差的余弦函数公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了计算能力和转化思想,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $(1,\sqrt{2}]$ | B. | $(-1,\sqrt{2}]$ | C. | $(-\sqrt{2},-1]$ | D. | $(-\sqrt{2},1]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
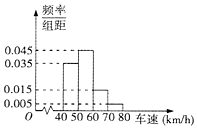 某市交管部门对一路段限速60km/h,为调查违章情况,对经过该路段的300辆汽车进行检测,将所得数据按[40,50),[50.60),[60,70),[70,80)(所有车辆的车速均在[40,80]内)分成四组,绘制成如图所示的频率分布直方图.
某市交管部门对一路段限速60km/h,为调查违章情况,对经过该路段的300辆汽车进行检测,将所得数据按[40,50),[50.60),[60,70),[70,80)(所有车辆的车速均在[40,80]内)分成四组,绘制成如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin($\frac{x}{2}$+$\frac{π}{6}$) | B. | y=cos(2x+$\frac{π}{3}$) | C. | y=sin(2x-$\frac{π}{6}$) | D. | y=cos(2x-$\frac{π}{6}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 抽签法 | B. | 分层抽样 | C. | 系统抽样 | D. | 随机数表法 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\root{3}{4}$ | B. | $\root{3}{4}$ | C. | 4$\root{3}{3}$ | D. | $\root{3}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com