
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,且过点
,且过点![]() .
.
(1)求C的方程;
(2)若直线l与C有且只有一个公共点,l与圆x2+y2=6交于A,B两点,直线OA,OB的斜率分别记为k1,k2.试判断k1k2是否为定值,若是,求出该定值;否则,请说明理由.
【答案】(1)![]() ;(2)k1k2为定值
;(2)k1k2为定值![]() .
.
【解析】
(1)由题意可得关于a,b,c的方程组,求解a,b,c的值,即可得到椭圆的方程;
(2)①当过点P的直线斜率不存在时,直线的方程为x=±2,求得![]() ,②当过P的直线斜率存在时,设其方程为y=kx+m,联立直线方程与椭圆方程,由判别式等于0可得m2=4k2+2,联立直线方程与椭圆方程,利用根与系数的关系结合斜率公式可得
,②当过P的直线斜率存在时,设其方程为y=kx+m,联立直线方程与椭圆方程,由判别式等于0可得m2=4k2+2,联立直线方程与椭圆方程,利用根与系数的关系结合斜率公式可得![]() 为定值
为定值![]() .
.
(1)由题意,得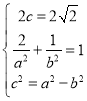 ,
,
解得![]() .
.
∴椭圆C的方程为![]() .
.
(2)k1k2为定值![]()
理由如下:
①当过点P的直线斜率不存在时,直线的方程为x=±2;
当x=2时,![]() ,则
,则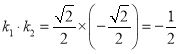 ,
,
当![]() 时,
时,![]() ,则
,则![]() .
.
②当过P的直线斜率存在时,设其方程为![]() ,
,
联立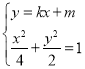 ,得
,得![]()
由题意![]() ,得
,得![]() ,
,
联立![]() ,得
,得![]()
则![]()
所以![]()
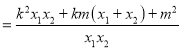
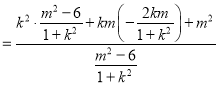
![]()
![]()
综上,![]() 为定值
为定值![]() .
.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的方程
的方程![]() ,焦点为
,焦点为![]() ,已知点
,已知点![]() 在
在![]() 上,且点
上,且点![]() 到点
到点![]() 的距离比它到
的距离比它到![]() 轴的距离大1.
轴的距离大1.
(1)试求出抛物线![]() 的方程;
的方程;
(2)若抛物线![]() 上存在两动点
上存在两动点![]() (
(![]() 在对称轴两侧),满足
在对称轴两侧),满足![]() (
(![]() 为坐标原点),过点
为坐标原点),过点![]() 作直线交
作直线交![]() 于
于![]() 两点,若
两点,若![]() ,线段
,线段![]() 上是否存在定点
上是否存在定点![]() ,使得
,使得![]() 恒成立?若存在,请求出
恒成立?若存在,请求出![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知在算法中“![]() ”和“
”和“![]() ”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑洞”(即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入
”分别表示取商和取余数.为了验证三位数卡普雷卡尔“数字黑洞”(即输入一个无重复数字的三位数,经过如图的有限次的重排求差计算,结果都为495).小明输入![]() ,则输出的
,则输出的![]() ( )
( )![]()
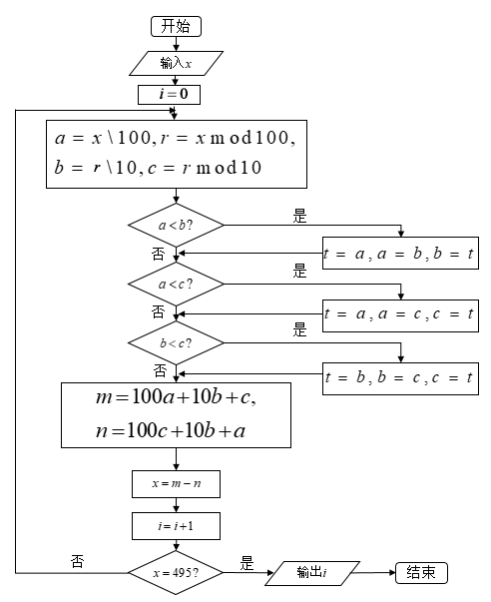
A.3B.4C.5D.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2021年开始,我省将试行“3+1+2“的普通高考新模式,即除语文、数学、外语3门必选科目外,考生再从物理、历史中选1门,从化学、生物、地理、政治中选2门作为选考科目.为了帮助学生合理选科,某中学将高一每个学生的六门科目综合成绩按比例均缩放成5分制,绘制成雷达图.甲同学的成绩雷达图如图所示,下面叙述一定不正确的是( )

A.甲的物理成绩领先年级平均分最多
B.甲有2个科目的成绩低于年级平均分
C.甲的成绩从高到低的前3个科目依次是地理、化学、历史
D.对甲而言,物理、化学、地理是比较理想的一种选科结果
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{![]() }的首项a1=2,前n项和为
}的首项a1=2,前n项和为![]() ,且数列{
,且数列{![]() }是以
}是以![]() 为公差的等差数列·
为公差的等差数列·
(1)求数列{![]() }的通项公式;
}的通项公式;
(2)设![]() ,
,![]() ,数列{
,数列{![]() }的前n项和为
}的前n项和为![]() ,
,
①求证:数列{![]() }为等比数列,
}为等比数列,
②若存在整数m,n(m>n>1),使得![]() ,其中
,其中![]() 为常数,且
为常数,且![]() -2,求
-2,求![]() 的所有可能值.
的所有可能值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两个快递公司的工作状况,假设同一个公司快递员的工作状况基本相同,现从甲、乙两公司各随机抽取一名快递员,并从两人某月(30天)的快递件数记录结果中随机抽取10天的数据,制表如图:

每名快递员完成一件货物投递可获得的劳务费情况如下:甲公司规定每件4.5元;乙公司规定每天35件以内(含35件)的部分每件4元,超出35件的部分每件7元.
(1)根据表中数据写出甲公司员工A在这10天投递的快递件数的平均数和众数;
(2)为了解乙公司员工B的每天所得劳务费的情况,从这10天中随机抽取1天,他所得的劳务费记为X(单位:元),求X的分布列和数学期望;
(3)根据表中数据估算两公司的每位员工在该月所得的劳务费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com