
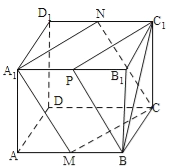
【题目】如图所示,在棱长为2的正方体![]() 中,
中,![]() 的中点是P,过点
的中点是P,过点![]() 作与截面
作与截面![]() 平行的截面,则截面的面积为__________.
平行的截面,则截面的面积为__________.

【答案】![]()
【解析】
试题取AB、C1D1的中点M、N,连结A1M、MC、CN、NA1.由已知得四边形A1MCN是平行四边形,连结MN,作A1H⊥MN于H,由题意能求出截面的面积.
解:取AB、C1D1的中点M、N,连结A1M、MC、CN、NA1.
由于A1N∥PC1∥MC且A1N=PC1=MC,
∴四边形A1MCN是平行四边形.
又∵A1N∥PC1,A1M∥BP,A1N∩A1M=A1,
PC1∩BP=P,
∴平面A1MCN∥平面PBC1
因此,过A1点作与截面PBC1平行的截面是平行四边形.
又连结MN,作A1H⊥MN于H,由于A1M=A1N=![]() ,MN=2
,MN=2![]() ,
,
则AH=![]() .
.
∴![]() =
=![]() ,
,
故![]() =2
=2![]() =2
=2![]() .
.
故答案为![]() .
.


科目:高中数学 来源: 题型:
【题目】对某校高三年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数,根据此数据作出了频数与频率的统计表和频率分布直方图.
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 24 | n |
[20,25) | m | p |
[25,30] | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间[10,15)内的人数;
(3)估计这次学生参加社区服务人数的众数、中位数以及平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a,b∈R,关于x的方程(x2﹣ax+1)(x2﹣bx+1)=0的四个实根构成以q为公比的等比数列,若q∈[![]() ,2],则ab的取值范围为______.
,2],则ab的取值范围为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,直线
,直线![]() :
:![]() 与以原点为圆心,以椭圆
与以原点为圆心,以椭圆![]() 的短半轴长为半径的圆相切.
的短半轴长为半径的圆相切.![]() 为左顶点,过点
为左顶点,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点.
两点.
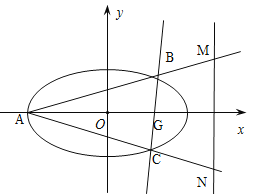
(1)求椭圆![]() 的方程;
的方程;
(2)以线段![]() 为直径的圆是否过定点?若是,写出所有定点的坐标;若不是,请说明理由.
为直径的圆是否过定点?若是,写出所有定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ADC=60°,侧面PDC是正三角形,平面PDC⊥平面ABCD,CD=2,M为PB的中点.

(1)求证:PA⊥平面CDM.
(2)求二面角D-MC-B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,直线![]() 将矩形纸
将矩形纸![]() 分为两个直角梯形
分为两个直角梯形![]() 和
和![]() ,将梯形
,将梯形![]() 沿边
沿边![]() 翻折,如图2,在翻折的过程中(平面
翻折,如图2,在翻折的过程中(平面![]() 和平面
和平面![]() 不重合),下面说法正确的是
不重合),下面说法正确的是
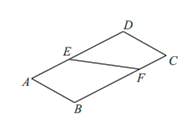
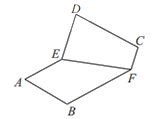
图1 图2
A.存在某一位置,使得![]() 平面
平面![]()
B.存在某一位置,使得![]() 平面
平面![]()
C.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
D.在翻折的过程中,![]() 平面
平面![]() 恒成立
恒成立
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“和、平、世、界”四个字,有放回地从中任取一个小球,直到”和””平”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“和、平、世、界”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下24个随机数组:
232 321 230 023 123 021 132 220 011 203 331 100
231 130 133 231 031 320 122 103 233 221 020 132
由此可以估计,恰好第三次就停止的概率为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com