方程ax2+2x+1=0至少有一个负的实数根的充要条件是( )
A.0<a<1
B.0<a≤1或a<0
C.0≤a≤1
D.a≤1
【答案】
分析:根据所给的方程的特征项的系数是一个字母,需要先对二次项系数分为0和不为0两种情况讨论,在二次项系数不为0时又分两根一正一负和两根均为负值两种情况,综合在一起找到a所满足的条件a≤1.
解答:解:当a=0得到
x=-

符合题意.
当a≠0时,显然方程没有等于零的根.
若方程有两异号实根,根据根与系数之间的关系得到a<0;
若方程有两个负的实根,
由根与系数之间的关系得到
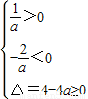
∴0<a≤1.
综上知,若方程至少有一个负实根,则a≤1.
∴关于x的方程ax
2+2x+1=0至少有一负的实根的充要条件是a≤1.
故选D.
点评:本题考查一元二次方程实根分布问题即充要条件问题,本题解题的关键是对于特征项的系数等于0的情况不要忽略,要熟练应用根与系数的关系,本题是一个易错题.

 符合题意.
符合题意.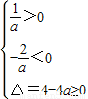


 名校课堂系列答案
名校课堂系列答案