
| A. | $α≤\frac{π}{3}$且$sinβ≤\frac{{\sqrt{3}}}{3}$ | B. | $α≤\frac{π}{3}$且$sinβ<\frac{{\sqrt{3}}}{3}$ | C. | $α≤\frac{π}{6}$且$β≥\frac{π}{3}$ | D. | $α≤\frac{π}{6}$且$β<\frac{π}{3}$ |
分析 可设BC=a,可得AB=PB=2a,AC=CP=$\sqrt{3}$a,过C作CH⊥平面PAB,连接HB,则PC与平面PAB所成角为β=∠CPH,由CH<CB,可得sinβ的范围;由二面角的定义,可得二面角P-BC-A大小为θ,即为∠ACP,设P到平面ABC的距离为d,根据等积法和正弦函数的定义和性质,即可得到PB与平面ABC所成角α的范围.
解答 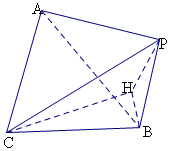 解:在△ABC中,∠ACB=$\frac{π}{2}$,AB=2BC,
解:在△ABC中,∠ACB=$\frac{π}{2}$,AB=2BC,
可设BC=a,可得AB=PB=2a,AC=CP=$\sqrt{3}$a,
过C作CH⊥平面PAB,连接HB,
则PC与平面PAB所成角为β=∠CPH,
且CH<CB=a,
sinβ=$\frac{CH}{CP}$<$\frac{a}{\sqrt{3}a}$=$\frac{\sqrt{3}}{3}$;
由BC⊥AC,BC⊥CP,
可得二面角P-BC-A大小为θ,即为∠ACP,
设P到平面ABC的距离为d,
由BC⊥平面PAC,
且VB-ACP=VP-ABC,
即有$\frac{1}{3}$BC•S△ACP=$\frac{1}{3}$d•S△ABC,
即$\frac{1}{3}$a•$\frac{1}{2}$•$\sqrt{3}$a•$\sqrt{3}$a•sinθ=$\frac{1}{3}$d•$\frac{1}{2}$•$\sqrt{3}$a•a,
解得d=$\sqrt{3}$sinθ,
则sinα=$\frac{d}{PB}$=$\frac{\sqrt{3}asinθ}{2a}$≤$\frac{\sqrt{3}}{2}$,
即有α≤$\frac{π}{3}$.
故选:B.
点评 本题考查空间的二面角和线面角的求法,注意运用定义和转化思想,以及等积法,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
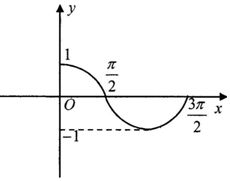 已知函数f(x)=sin(ωx+φ),x∈R(其中ω>0,-π<φ<π)的部分图象,如图所示.那么f(x)的解析式为( )
已知函数f(x)=sin(ωx+φ),x∈R(其中ω>0,-π<φ<π)的部分图象,如图所示.那么f(x)的解析式为( )| A. | $f(x)=sin(x+\frac{π}{2})$ | B. | $f(x)=sin(x-\frac{π}{2})$ | C. | $f(x)=sin(2x+\frac{π}{2})$ | D. | $f(x)=sin(2x-\frac{π}{2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{6}+\frac{y^2}{4}=1$ | B. | $\frac{x^2}{16}+\frac{y^2}{36}=1$ | C. | $\frac{x^2}{36}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{49}+\frac{y^2}{9}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com