
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() ),
),![]() 和
和![]() 是函数
是函数![]() 的图象与
的图象与![]() 轴的2个相邻交点的横坐标,且当
轴的2个相邻交点的横坐标,且当![]() 时,
时,![]() 取得最大值2.
取得最大值2.
(1)求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)将函数![]() 的图象上的每一点的横坐标变为原来的
的图象上的每一点的横坐标变为原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象,再将函数
的图象,再将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求函数
的图象,求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】某中学为了解高二年级中华传统文化经典阅读的整体情况,从高二年级随机抽取10名学生进行了两轮测试,并把两轮测试成绩的平均分作为该名学生的考核成绩.记录的数据如下:
1号 | 2号 | 3号 | 4号 | 5号 | 6号 | 7号 | 8号 | 9号 | 10号 | |
第一轮测试成绩 | 96 | 89 | 88 | 88 | 92 | 90 | 87 | 90 | 92 | 90 |
第二轮测试成绩 | 90 | 90 | 90 | 88 | 88 | 87 | 96 | 92 | 89 | 92 |
(Ⅰ)从该校高二年级随机选取一名学生,试估计这名学生考核成绩大于90 分的概率;
(Ⅱ)从考核成绩大于90分的学生中再随机抽取两名同学,求这两名同学两轮测试成绩均大于等于90分的概率;
(Ⅲ)记抽取的10名学生第一轮测试的平均数和方差分别为![]() ,
,![]() ,考核成绩的平均数和方差分别为
,考核成绩的平均数和方差分别为![]() ,
,![]() ,试比较
,试比较![]() 与
与![]() ,
, ![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆柱体木材的横截面半径为![]() ,从该木材中截取一段圆柱体,再加工制作成直四棱柱
,从该木材中截取一段圆柱体,再加工制作成直四棱柱![]() ,该四棱柱的上、下底面均为等腰梯形,分别内接于圆柱的上、下底面,下底面圆的圆心
,该四棱柱的上、下底面均为等腰梯形,分别内接于圆柱的上、下底面,下底面圆的圆心![]() 在梯形
在梯形![]() 内部,
内部,![]() ,
,![]() ,
,![]() ,设
,设![]() .
.
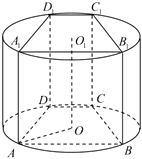
(1)求梯形![]() 的面积;
的面积;
(2)当![]() 取何值时,直四棱柱
取何值时,直四棱柱![]() 的体积最大?并求出最大值(注:木材的长度足够长)
的体积最大?并求出最大值(注:木材的长度足够长)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() 且右焦点
且右焦点![]() 到右准线
到右准线![]() 的距离为
的距离为![]() .
.
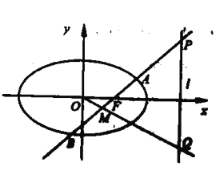
(1)求椭圆![]() 的标准方程:
的标准方程:
(2)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() 两点,与
两点,与![]() 交于点
交于点![]() 是弦
是弦![]() 的中点,直线
的中点,直线![]() 与
与![]() 交于点
交于点![]() .若
.若![]() 与
与![]() 的面积之比是
的面积之比是![]() ,求
,求![]() 的长度.
的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的参数方程为![]() (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为![]() .
.
(1)直线l与曲线C是否有公共点?并说明理由;
(2)若直线l与两坐标轴的交点为A,B,点P是曲线C上的一点,求△PAB的面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市美团外卖配送员底薪是每月1800元,设每月配送单数为X,若![]() ,每单提成3元,若
,每单提成3元,若![]() ,每单提成4元,若
,每单提成4元,若![]() ,每单提成4.5元,饿了么外卖配送员底薪是每月2100元,设每月配送单数为Y,若
,每单提成4.5元,饿了么外卖配送员底薪是每月2100元,设每月配送单数为Y,若![]() ,每单提成3元,若
,每单提成3元,若![]() ,每单提成4元,小想在美团外卖和饿了么外卖之间选择一份配送员工作,他随机调查了美团外卖配送员甲和饿了么外卖配送员乙在2019年4月份(30天)的送餐量数据,如下表:
,每单提成4元,小想在美团外卖和饿了么外卖之间选择一份配送员工作,他随机调查了美团外卖配送员甲和饿了么外卖配送员乙在2019年4月份(30天)的送餐量数据,如下表:
表1:美团外卖配送员甲送餐量统计
日送餐量x(单) | 13 | 14 | 16 | 17 | 18 | 20 |
天数 | 2 | 6 | 12 | 6 | 2 | 2 |
表2:饿了么外卖配送员乙送餐量统计
日送餐量x(单) | 11 | 13 | 14 | 15 | 16 | 18 |
天数 | 4 | 5 | 12 | 3 | 5 | 1 |
(1)设美团外卖配送员月工资为![]() ,饿了么外卖配送员月工资为
,饿了么外卖配送员月工资为![]() ,当
,当![]() 时,比较
时,比较![]() 与
与![]() 的大小关系
的大小关系
(2)将4月份的日送餐量的频率视为日送餐量的概率
(ⅰ)计算外卖配送员甲和乙每日送餐量的数学期望E(X)和E(Y)
(ⅱ)请利用所学的统计学知识为小王作出选择,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com