
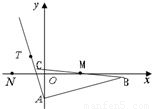
 已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足
已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足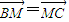 ,点T(-1,1)在AC所在直线上且
,点T(-1,1)在AC所在直线上且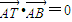 .
. 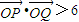 ,求k的取值范围.
,求k的取值范围.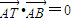 ,知AT⊥AB,从而直线AC的斜率为-3.所以AC边所在直线的方程为3x+y+2=0.由
,知AT⊥AB,从而直线AC的斜率为-3.所以AC边所在直线的方程为3x+y+2=0.由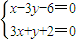 得点A的坐标为(0,-2),由此能求出△ABC外接圆的方程.
得点A的坐标为(0,-2),由此能求出△ABC外接圆的方程.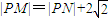 ,即
,即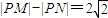 .故点P的轨迹是以M,N为焦点,实轴长为
.故点P的轨迹是以M,N为焦点,实轴长为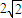 ,半焦距c=2的双曲线的左支.由此能求出动圆圆心的轨迹方程.
,半焦距c=2的双曲线的左支.由此能求出动圆圆心的轨迹方程.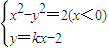 得(1-k2)x2+4kx-6=0(x<0)
得(1-k2)x2+4kx-6=0(x<0)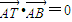 ∴AT⊥AB,从而直线AC的斜率为-3.
∴AT⊥AB,从而直线AC的斜率为-3.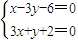 得点A的坐标为(0,-2),
得点A的坐标为(0,-2),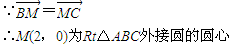
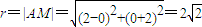 .
.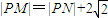 ,即
,即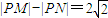 .
.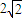 ,半焦距c=2的双曲线的左支.
,半焦距c=2的双曲线的左支.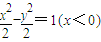 .
.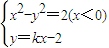 得(1-k2)x2+4kx-6=0(x<0)
得(1-k2)x2+4kx-6=0(x<0)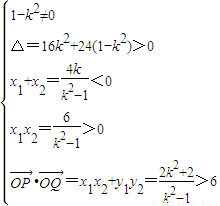


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
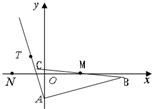 已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足
已知△ABC的边AB所在直线的方程为x-3y-6=0,M(2,0)满足| BM |
| MC |
| AT |
| AB |
| OP |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
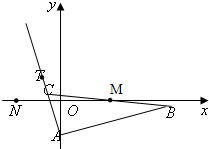 已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足
已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足| BM |
| MC |
| AT |
| AB |
| n |
 |
| i=k |
查看答案和解析>>
科目:高中数学 来源: 题型:
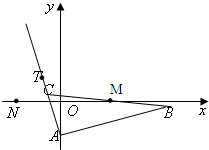 已知△ABC的边AB边所在直线的方程为x-3y-6=0点B关于点M(2,0)的对称点为C,点T(-1,1)在AC边所在直线上且满足
已知△ABC的边AB边所在直线的方程为x-3y-6=0点B关于点M(2,0)的对称点为C,点T(-1,1)在AC边所在直线上且满足| AT |
| AB |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•东莞二模)已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足
(2012•东莞二模)已知△ABC的边AB边所在直线的方程为x-3y-6=0,M(2,0)满足| BM |
| MC |
| AT |
| AB |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省徐州市运河中学高三摸底迎考练习(二)(解析版) 题型:解答题
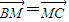 ,点T(-1,1)在AC边所在直线上且满足
,点T(-1,1)在AC边所在直线上且满足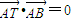 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com