
【题目】在长方体![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是棱
分别是棱![]() 的中点,
的中点,![]() 是底面
是底面![]() 内一动点,若直线
内一动点,若直线![]() 与平面
与平面![]() 平行,则三角形
平行,则三角形![]() 面积最小值为( )
面积最小值为( )
A.![]() B.1C.
B.1C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】自由购是通过自助结算方式购物的一种形式.某大型超市为调查顾客使用自由购的情况,随机抽取了100人,统计结果整理如下:
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
(Ⅰ)现随机抽取1名顾客,试估计该顾客年龄在![]() 且未使用自由购的概率;
且未使用自由购的概率;
(Ⅱ)从被抽取的年龄在![]() 使用自由购的顾客中,随机抽取3人进一步了解情况,用
使用自由购的顾客中,随机抽取3人进一步了解情况,用![]() 表示这3人中年龄在
表示这3人中年龄在![]() 的人数,求随机变量
的人数,求随机变量![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅲ)为鼓励顾客使用自由购,该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物,试估计该超市当天至少应准备多少个环保购物袋.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙三人参加微信群抢红包游戏,规则如下:每轮游戏发![]() 个红包,每个红包金额为
个红包,每个红包金额为![]() 元,
元,![]() .已知在每轮游戏中所产生的
.已知在每轮游戏中所产生的![]() 个红包金额的频率分布直方图如图所示.
个红包金额的频率分布直方图如图所示.
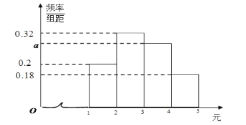
(1)求![]() 的值,并根据频率分布直方图,估计红包金额的众数;
的值,并根据频率分布直方图,估计红包金额的众数;
(2)以频率分布直方图中的频率作为概率,若甲、乙、丙三人从中各抢到一个红包,其中金额在![]() 的红包个数为
的红包个数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C在⊙O上,且∠AOC=120°,PA⊥平面ABC,AB=4,PA=2![]() ,D是PC的中点,点M是⊙O上的动点(不与A,C重合).
,D是PC的中点,点M是⊙O上的动点(不与A,C重合).
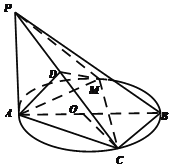
(1)证明:AD⊥PB;
(2)当三棱锥D﹣ACM体积最大时,求面MAD与面MCD所成二面角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《最强大脑》是大型科学竞技类真人秀节目,是专注传播脑科学知识和脑力竞技的节目.某机构为了了解大学生喜欢《最强大脑》是否与性别有关,对某校的100名大学生进行了问卷调查,得到如下列联表:
喜欢《最强大脑》 | 不喜欢《最强大脑》 | 合计 | |
男生 | 15 | ||
女生 | 15 | ||
合计 |
已知在这100人中随机抽取1人抽到不喜欢《最强大脑》的大学生的概率为0.4
(I)请将上述列联表补充完整;判断是否有99.9%的把握认为喜欢《最强大脑》与性别有关,并说明理由;
(II)已知在被调查的大学生中有5名是大一学生,其中3名喜欢《最强大脑》,现从这5名大一学生中随机抽取2人,抽到喜欢《最强大脑》的人数为X,求X的分布列及数学期望.
参考公式: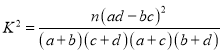 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
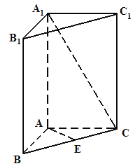
【题目】如图,直三棱柱![]() 的底面
的底面![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,侧棱
,侧棱![]() 底面
底面![]() ,且
,且![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求直三棱柱![]() 的全面积;
的全面积;
(2)求异面直线![]() 与
与![]() 所成角
所成角![]() 的大小(结果用反三角函数表示);
的大小(结果用反三角函数表示);
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 和
和![]() 的项数均为
的项数均为![]() ,则将两个数列的偏差距离定义为
,则将两个数列的偏差距离定义为![]() ,其中
,其中![]() .
.
(1)求数列1,2,7,8和数列2,3,5,6的偏差距离;
(2)设![]() 为满足递推关系
为满足递推关系![]() 的所有数列
的所有数列![]() 的集合,
的集合,![]() 和
和![]() 为
为![]() 中的两个元素,且项数均为
中的两个元素,且项数均为![]() ,若
,若![]() ,
,![]() ,
,![]() 和
和![]() 的偏差距离小于2020,求
的偏差距离小于2020,求![]() 最大值;
最大值;
(3)记![]() 是所有7项数列
是所有7项数列![]() 或
或![]() 的集合,
的集合,![]() ,且
,且![]() 中任何两个元素的偏差距离大于或等于3,证明:
中任何两个元素的偏差距离大于或等于3,证明:![]() 中的元素个数小于或等于16.
中的元素个数小于或等于16.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com