
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点.
的中点.
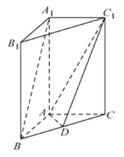
(1)求证:![]() 面
面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1) 略 (2)1/3
【解析】
试题分析:(1)建立空间直角坐标系,求出平面ADC1的法向量,证明![]() =2×2+0×(2)+(4)×1=0,即可证明A1B∥面ADC1;(2)求出:
=2×2+0×(2)+(4)×1=0,即可证明A1B∥面ADC1;(2)求出:![]() =(2,2,0),利用向量的夹角公式,即可求直线
=(2,2,0),利用向量的夹角公式,即可求直线![]() 与平面
与平面![]() 所成角的余弦值
所成角的余弦值
试题解析:(1)证明:如图,以{AB,AC,AA1}为单位正交基底建立空间直角坐标系A-xyz,
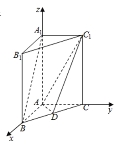
则A(0,0,0),B(2,0,0),C(0,2,0),A1(0,0,4),D(1,1,0),B1(2,0,4),C1(0,2,4)
∴![]() =(2,0,4),
=(2,0,4),![]() =(1,1,0),
=(1,1,0),![]() =(0,2,4),
=(0,2,4),
设平面![]() 的法向量为
的法向量为![]() =(x,y,z),由
=(x,y,z),由![]()
∴![]() 取z=1,得y=-2,x=2,∴平面ADC1的法向量为
取z=1,得y=-2,x=2,∴平面ADC1的法向量为![]() =(2,2,1)
=(2,2,1)
由此可得,![]() =2×2+0×(2)+(4)×1=0,又A1B平面ADC1,∴A1B∥面ADC1.
=2×2+0×(2)+(4)×1=0,又A1B平面ADC1,∴A1B∥面ADC1.
(2)解:![]() =(2,2,0),设直线
=(2,2,0),设直线![]() 与平面
与平面![]() 所成角为θ,则
所成角为θ,则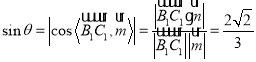 ,
,
又θ为锐角,∴直线![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的公比q>1,且满足a2+a3+a4=28,且a3+2是a2,a4的等差中项.
(1)求数列{an}的通项公式;
(2)若bn=log![]() ,Sn=b1+b2+…+bn,求使
,Sn=b1+b2+…+bn,求使![]() 成立的正整数n的最大值.
成立的正整数n的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等比数列{an}的公比为q,其前n项的积为Tn,并且满足条件a1>1,a49a50-1>0,(a49-1)(a50-1)<0.给出下列结论:
①0<q<1;②a1a99-1<0;③T49的值是Tn中最大的;④使Tn>1成立的最大自然数n等于98.
其中所有正确结论的序号是____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() 且满足
且满足![]() ,数列
,数列![]() 中,
中,![]() 对任意正整数
对任意正整数![]()
(1)求数列![]() 的通项公式;
的通项公式;
(2)是否存在实数![]() ,使得数列
,使得数列![]() 是等比数列?若存在,请求出实数
是等比数列?若存在,请求出实数![]() 及公比
及公比![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了对某课题进行研究,用分层抽样方法从三所高校![]() 的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
高校 | 相关人数 | 抽取人数 |
A | 18 |
|
B | 36 | 2 |
C | 54 |
|
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)若从高校![]() 抽取的人中选2人作专题发言,求这二人都来自高校
抽取的人中选2人作专题发言,求这二人都来自高校![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与直线
与直线![]() 相切.
相切.
(1)求圆![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 截圆
截圆![]() 所得弦长为
所得弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)设圆![]() 与
与![]() 轴的负半抽的交点为
轴的负半抽的交点为![]() ,过点
,过点![]() 作两条斜率分别为
作两条斜率分别为![]() 的直线交圆
的直线交圆![]() 于
于![]() 两点,且
两点,且![]() ,证明:直线
,证明:直线![]() 过定点,并求出该定点坐标.
过定点,并求出该定点坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题P;实数x满足x2-4ax+3a2<0,其中a>0;命题q:实数x满足x2-5x+6≤0
(1)若a=1,且![]() 为真命题,求实数x的取值范围。
为真命题,求实数x的取值范围。
(2)若p是q成立的必要不充分条件,求实数a 的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,某城市有一块半径为40![]() 的半圆形(以
的半圆形(以![]() 为圆心,
为圆心,![]() 为直径)绿化区域,现计划对其进行改建,在
为直径)绿化区域,现计划对其进行改建,在![]() 的延长线上取点
的延长线上取点![]() ,使
,使![]() ,在半圆上选定一点
,在半圆上选定一点![]() ,改建后的绿化区域由扇形区域
,改建后的绿化区域由扇形区域![]() 和三角形区域
和三角形区域![]() 组成,其面积为
组成,其面积为![]() ,设
,设![]()
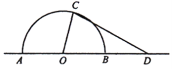
(1)写出![]() 关于
关于![]() 的函数关系式
的函数关系式![]() ,并指出
,并指出![]() 的取值范围;
的取值范围;
(2)试问![]() 多大时,改建后的绿化区域面积
多大时,改建后的绿化区域面积![]() 最大.
最大.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com