练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知公比为负值的等比数列{an}中，a1a5=4，a4=﹣1．
    （1）求数列{an}的通项公式；
    （2）设bn= + +…+ ，求数列{an+bn}的前n项和Sn ．

    【答案】
    （1）解：设等比数列{an}的公比为q＜0，

    ∵a1a5=4，a4=﹣1．

    ∴ ， =﹣1，解得q=﹣ ，a1=8．

    ∴ =


    （2）解：∵bn= + +…+

    =（n+1）[ +…+ ]

    =（n+1）× =n，

    ∴an+bn= +n，

    其前n项和Sn= + = +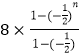


    【解析】（1）设等比数列{an}的公比为q＜0，由a1a5=4，a4=﹣1．可得 ， =﹣1，解得即可；（2）由bn= + +…+ =（n+1）[ +…+ ]=n，可得an+bn= +n，再利用等差数列与等比数列的前n项和公式即可得出．
    【考点精析】认真审题，首先需要了解等比数列的通项公式（及其变式）(通项公式：)，还要掌握数列的前n项和(数列{an}的前n项和sn与通项an的关系)的相关知识才是答题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知是首项为19，公差为-2的等差数列，为的前项和．

    （1）求通项及；

    （2）设是首项为1，公比为3的等比数列，求数列的通项公式及其前项和．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π），在同一周期内，当x= 时，f（x）取得最大值3；当x= 时，f（x）取得最小值﹣3．
    （1）求函数f（x）的解析式；
    （2）求函数f（x）的单调递减区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（， =2.718………），

    （I） 当时，求函数的单调区间；

    （II）当时，不等式对任意恒成立，

    求实数的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知四棱锥的底面是平行四边形， 平面， 是的中点， 是的中点．

    （1）求证： 平面；

    （2）若，求证：平面平面．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图， 是圆的直径，点是圆上异于、的点，直线度平面， 、分别是、的中点．

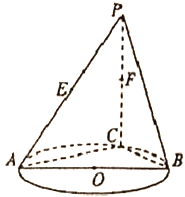
    （Ⅰ）设平面与平面的交线为，求直线与平面所成角的余弦值；

    （Ⅱ）设（Ⅰ）中的直线与圆的另一个交点为点，且满足， ，当二面角的余弦值为时，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，矩形中， ， 为边的中点，将沿直线翻转成.若为线段的中点，则在翻折过程中：

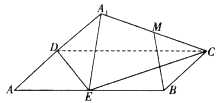
    ①是定值；②点在某个球面上运动；

    ③存在某个位置，使；④存在某个位置，使平面.

    其中正确的命题是_________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某同学用“随机模拟方法”计算曲线与直线， 所围成的曲边三角形的面积时，用计算机分别产生了10个在区间上的均匀随机数和10个区间上的均匀随机数（， ），其数据如下表的前两行.

    2.50

    1.01

    1.90

    1.22

    2.52

    2.17

    1.89

    1.96

    1.36

    2.22

    0.84

    0.25

    0.98

    0.15

    0.01

    0.60

    0.59

    0.88

    0.84

    0.10

    0.90

    0.01

    0.64

    0.20

    0.92

    0.77

    0.64

    0.67

    0.31

    0.80

    由此可得这个曲边三角形面积的一个近似值是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数f（x）=ax2+bx+c．
    （1）若f（﹣1）=0，试判断函数f（x）零点个数；
    （2）若对x1x2∈R，且x1＜x2 ， f（x1）≠f（x2），证明方程f（x）= 必有一个实数根属于（x1 ， x2）．
    （3）是否存在a，b，c∈R，使f（x）同时满足以下条件
    ①当x=﹣1时，函数f（x）有最小值0；
    ②对任意x∈R，都有0≤f（x）﹣x≤ 若存在，求出a，b，c的值，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案