
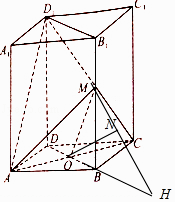
【题目】如图,长方体ABCD﹣A1B1C1D1中,点M在棱BB1上,两条直线MA,MC与平面ABCD所成角均为θ,AC与BD交于点O. 
(1)求证:AC⊥OM;
(2)当M为BB1的中点,且θ= ![]() 时,求二面角A﹣D1M﹣B1的余弦值.
时,求二面角A﹣D1M﹣B1的余弦值.
【答案】
(1)证明:∵MB⊥面ABCD,直线MA,MC与平面ABCD所成角均为θ,∴∠MAB=∠MCB=θ.
故△MBA≌MBC,BA=BC.
∴四边形ABCD为正方形,AC⊥DB,又AC⊥MB,DB∩MB=B
∴AC⊥面BDM,即AC⊥OM
(2)解:θ= ![]() 时,则有AB=BC=MB,延长D1M,DB交于点点H,
时,则有AB=BC=MB,延长D1M,DB交于点点H,
过点O作ON⊥D1H于点N,连接AN,则∠ANO为二面角A﹣D1M﹣B的平面角.
设AB=1,由△D1DH∽△ONH易得ON= ![]() ,AO=
,AO= ![]() ,
,
tan∠ANO= ![]() ,∴∠ANO=30°
,∴∠ANO=30°
二面角A﹣D1M﹣B1的余弦值为 ![]() .
.
【解析】(Ⅰ)由 MC与平面ABCD所成角均为θ,得∠MAB=∠MCB=θ.BA=BC.四边形ABCD为正方形,即可得AC⊥面BDM,即AC⊥OM.(Ⅱ) θ= ![]() 时,则有AB=BC=MB,延长D1M,DB交于点点H,过点O作ON⊥D1H于点N,连接AN,则∠ANO为二面角A﹣D1M﹣B的平面角,利用平面几何知识即可求解.
时,则有AB=BC=MB,延长D1M,DB交于点点H,过点O作ON⊥D1H于点N,连接AN,则∠ANO为二面角A﹣D1M﹣B的平面角,利用平面几何知识即可求解.
【考点精析】解答此题的关键在于理解直线与平面垂直的性质的相关知识,掌握垂直于同一个平面的两条直线平行.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)满足:f( ![]() +x)=﹣f(
+x)=﹣f( ![]() ﹣x),且f(
﹣x),且f( ![]() +x)=f(
+x)=f( ![]() ﹣x),则ω的一个可能取值是( )
﹣x),则ω的一个可能取值是( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图所示.

(1)求直方图中x的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为[220,240),[240,260),[260,280),[280,300]的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的4个图像中,与所给3个事件最吻合的顺序为
①我离开家后,心情愉快,缓慢行进,但最后发现快迟到时,加速前进;
②我骑着自行车上学,但中途车坏了,我修理好又以原来的速度前进;
③我快速的骑着自行车,最后发现时间充足,又减缓了速度.

① ② ③ ④
A. ③①② B. ③④② C. ②①③ D. ②④③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】总体由编号为01,02,…![]() ,19,20的20个个体组成,利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始从左到右依次选取两个数字,则选出来的第5个个体的编号为_______
,19,20的20个个体组成,利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第9列和第10列数字开始从左到右依次选取两个数字,则选出来的第5个个体的编号为_______
7816 6572 0802 6314 0702 4369 9728 0198
3204 9234 4935 8200 3623 4869 6938 7481
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆![]() 的半径为2,点
的半径为2,点![]() 是圆
是圆![]() 的六等分点中的五个点.
的六等分点中的五个点.

(1)从![]() 中随机取三点构成三角形,求这三点构成的三角形是直角三角形的概率;
中随机取三点构成三角形,求这三点构成的三角形是直角三角形的概率;
(2)在圆![]() 上随机取一点
上随机取一点![]() ,求
,求![]() 的面积大于
的面积大于![]() 的概率
的概率
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com