练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列四个命题中，真命题的序号有 .（写出所有真命题的序号）

    ①若，则“”是“”成立的充分不必要条件；

    ②命题“使得”的否定是“均有”；

    ③命题“若，则或”的否命题是“若，则”；

    ④函数在区间上有且仅有一个零点.

    【答案】①②③④

    【解析】

    试题分析：对于①，当时，说明且，于得两边同乘可得，反过来当时，不一定有，如时，，所以“”是“”成立的充分不必要条件；对于②，根据特称命题的否定是全称命题可知：命题“使得”的否定是“均有”；对于③，根据否命题的定义：原命题为若则，则它的否命题为若则，所以：命题“若，则或”的否命题是“若，则”；对于④，因为函数的定义域为，所以，所以函数在单调递增，又，根据零点存在定理可知在区间至少存在一个零点，而在单调递增，所以在区间有且仅有一个零点.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，以为极点， 轴正半轴为极轴建立极坐标系，圆的极坐标方程为，直线的参数方程为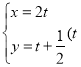为参数），直线和圆交于两点， 是圆上不同于的任意一点．

    （1）求圆心的极坐标；

    （2）求点到直线的距离的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学校本课程开设了A、B、C、D共4门选修课，每个学生必须且只能选修1门选修课，现有该校的甲、乙、丙3名学生：

    （Ⅰ）求这3名学生选修课所有选法的总数；

    （Ⅱ）求恰有2门选修课没有被这3名学生选择的概率；

    （Ⅲ）求A选修课被这3名学生选择的人数的分布列 .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现有4种不同颜色要对如图所示的四个部分进行着色，要求有公共边界的两部分不能用同一种颜色，则不同的着色方法共有（　　）

    A. 144种 B. 72种 C. 64种 D. 84种

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若关于某设备的使用年限x(年)和所支出的维修费y(万元)有如下统计资料：

    x

    2

    3

    4

    5

    6

    y

    2.2

    3.8

    5.5

    6.5

    7.0

    若由资料知，y对x呈线性相关关系．

    (1) 请根据上表提供的数据，用最小二乘法求出关于的线性回归方程 ；

    (2) 估计使用年限为10年时，试求维修费用约是多少？（精确到两位小数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】△ABC中，内角A，B，C的对边分别为a，b，c，2sin2 =sinC+1．
    （Ⅰ）求角C的大小；
    （Ⅱ）若a= ，c=1，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过抛物线y＝焦点F的直线交抛物线于A，B两点，点C在直线y＝－1上，若△ABC为正三角形，则其边长为

    A. 11 B. 13 C. 14 D. 12

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在极标坐系中，已知圆的圆心，半径

    （1）求圆的极坐标方程；

    （2）若，直线的参数方程为（t为参数），直线交圆于两点，求弦长的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列{an}满足a1= ，且an+1=an（an+1）（n∈N*），则m= + +…+ 的整数部分是（ ）
    A.0
    B.1
    C.2
    D.3

    查看答案和解析>>

    同步练习册答案