
【题目】某“![]() ” 型水渠南北向宽为
” 型水渠南北向宽为![]() ,东西向宽为
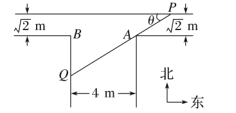
,东西向宽为![]() ,其俯视图如图所示.假设水渠内的水面始终保持水平位置.
,其俯视图如图所示.假设水渠内的水面始终保持水平位置.
(1) 过点![]() 的一条直线与水渠的内壁交于
的一条直线与水渠的内壁交于![]() 两点,且与水渠的一边的夹角为
两点,且与水渠的一边的夹角为![]() (
(![]() 为锐角),将线段
为锐角),将线段![]() 的长度
的长度![]() 表示为
表示为![]() 的函数;
的函数;
(2) 若从南面漂来一根长度为![]() 的笔直的竹竿(粗细不计),竹竿始终浮于水平面内,且不发生形变,问:这根竹竿能否从拐角处一直漂向东西向的水渠(不会卡住)?试说明理由.
的笔直的竹竿(粗细不计),竹竿始终浮于水平面内,且不发生形变,问:这根竹竿能否从拐角处一直漂向东西向的水渠(不会卡住)?试说明理由.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中以
中以![]() 为极点,
为极点,![]() 轴非负半轴为极轴建立坐标系圆
轴非负半轴为极轴建立坐标系圆![]() ,直线
,直线![]() 的极坐标方程分别
的极坐标方程分别
为![]() ,
,![]() .
.
(Ⅰ)求![]() 与
与![]() 交点的极坐标;
交点的极坐标;
(Ⅱ)设![]() 为
为![]() 的圆心,
的圆心, ![]() 为
为![]() 与
与![]() 交点连线的中点,已知直线
交点连线的中点,已知直线![]() 的参数方程为
的参数方程为
(![]() 为参数),求
为参数),求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高三模拟考试的学生中随机抽取![]() 名学生,将其数学成绩(均为整数)分成六段
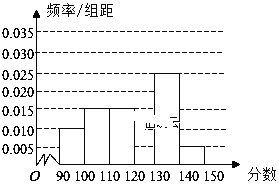
名学生,将其数学成绩(均为整数)分成六段![]() 后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
后得到如下部分频率分布直方图.观察图形的信息,回答下列问题:
(1)求分数在![]() 内的频率,补全这个频率分布直方图,并据此估计本次考试的平均分;
内的频率,补全这个频率分布直方图,并据此估计本次考试的平均分;
(2)用分层抽样的方法,在分数段为![]() 的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段
的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任取2个,求至多有1人在分数段![]() 内的概率
内的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,焦距为 2,一条准线方程为
,焦距为 2,一条准线方程为![]() ,
,![]() 为椭圆
为椭圆![]() 上一点,直线
上一点,直线![]() 交椭圆
交椭圆![]() 于另一点
于另一点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 的坐标为
的坐标为![]() ,求过
,求过![]() 三点的圆的方程;
三点的圆的方程;
(3)若![]() ,且
,且![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,将函数
,将函数![]() 的图象沿
的图象沿![]() 轴向左平移
轴向左平移![]() 个单位长度后,又沿
个单位长度后,又沿![]() 轴向上平移1个单位,再将得到的图象上各点的横坐标变为原来的
轴向上平移1个单位,再将得到的图象上各点的横坐标变为原来的![]() 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数![]() 的图象.
的图象.
(1)求![]() 的对称中心;
的对称中心;
(2)若![]() ,求
,求![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】莱市在市内主于道北京路一侧修建圆形休闲广场.如图,圆形广场的圆心为![]() ,半径为
,半径为![]() ,并与北京路一边所在直线
,并与北京路一边所在直线![]() 相切于点
相切于点![]() .点
.点![]() 为上半圆弧上一点,过点
为上半圆弧上一点,过点![]() 作
作![]() 的垂线,垂足为点
的垂线,垂足为点![]() .市园林局计划在
.市园林局计划在![]() 内进行绿化,设
内进行绿化,设![]() 的面积为
的面积为![]() (单位:
(单位:![]() ),
),![]() (单位:弧度).
(单位:弧度).

(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)当绿化面积![]() 最大时,试确定点
最大时,试确定点![]() 的位置,并求最大面积.
的位置,并求最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.某机构组织了一场诗词知识竞赛,将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,从中随机抽取100名选手进行调查,如图是根据调查结果绘制的选手等级与人数的条形图.
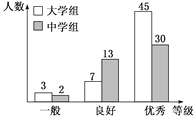
(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的2×2列联表,并据此判断能否在犯错误的概率不超过0.05的前提下认为选手成绩优秀与文化程度有关?
优秀 | 合格 | 总计 | |
大学组 | |||
中学组 | |||
总计 |
(2)若参赛选手共6万名,用频率估计概率,试估计其中优秀等级的选手人数;
(3)在优秀等级的选手中选取6名,在良好等级的选手中选取6名,都依次编号为1,2,3,4,5,6,在选出的6名优秀等级的选手中任取一名,记其编号为a,在选出的6名良好等级的选手中任取一名,记其编号为b,求使得方程组![]() 有唯一一组实数解(x,y)的概率.
有唯一一组实数解(x,y)的概率.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
P(K2≥k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com