
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的极值;
的极值;
(2)讨论![]() 的单调性.
的单调性.
【答案】(1)当![]() 时,
时,![]() 的极大值为9;当
的极大值为9;当![]() 时,的极小值为
时,的极小值为![]()
(2)①当![]() 时,
时,![]() 在R是增函数.
在R是增函数.
②当![]() 时,
时,![]() 的单调增区间为:
的单调增区间为:![]() ,
,![]() ;
;
单调减区间为:![]()
【解析】
(1)代入![]() ,求导后得
,求导后得![]() ,再列表分析各区间上导函数的正负与原函数的单调性与极值即可.
,再列表分析各区间上导函数的正负与原函数的单调性与极值即可.
(2)求导后![]() 再根据导函数有无零点讨论a的取值,再求解导数大于零,得递增区间,导数小于零得递减区间.
再根据导函数有无零点讨论a的取值,再求解导数大于零,得递增区间,导数小于零得递减区间.
解:(1)当![]() 时,
时,![]() ,则
,则![]()
令![]() 得
得![]() ,
,![]() 得
得![]() ,
,![]()
则x,![]() ,
,![]() 的关系如下:
的关系如下:
x |
|
|
| 1 |
|
|
| 0 |
| 0 |
|
| 增 | 9 | 减 |
| 增 |
所以,当![]() 时,
时,![]() 的极大值为9;当
的极大值为9;当![]() 时,的极小值为
时,的极小值为![]() .
.
(2)![]() ,
,
![]() ,
,
①当![]() 时,
时,![]() ,且仅当
,且仅当![]() ,
,![]() 时
时![]() ,所以
,所以![]() 在R是增函数,
在R是增函数,
②当![]() 时,
时,![]() 有两个根,
有两个根,![]() ,
,![]() ,
,
当![]() 时,得
时,得![]() 或
或![]() ,所以
,所以![]() 的单调增区间为:
的单调增区间为:![]() ,
,![]() ;
;
当![]() 时,得
时,得![]() ,所以
,所以![]() 的单调减区间为:
的单调减区间为:![]() .
.
综上所述, ①当![]() 时,
时,![]() 在R是增函数.
在R是增函数.
②当![]() 时,
时,![]() 的单调增区间为:
的单调增区间为:![]() ,
,![]() ;
;
单调减区间为:![]()


科目:高中数学 来源: 题型:
【题目】三棱柱![]() 中,
中,![]() 为
为![]() 的中点,点
的中点,点![]() 在侧棱
在侧棱![]() 上,
上,![]() 平面
平面![]()
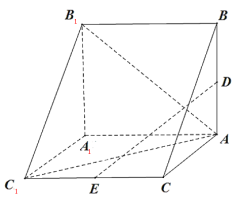
(1) 证明:![]() 是
是![]() 的中点;
的中点;
(2) 设![]() ,四边形
,四边形![]() 为边长为4正方形,四边形
为边长为4正方形,四边形![]() 为矩形,且异面直线
为矩形,且异面直线![]() 与
与![]() 所成的角为
所成的角为![]() ,求该三棱柱
,求该三棱柱![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】东西向的铁路上有两个道口![]() 、
、![]() ,铁路两侧的公路分布如图,
,铁路两侧的公路分布如图,![]() 位于
位于![]() 的南偏西
的南偏西![]() ,且位于
,且位于![]() 的南偏东
的南偏东![]() 方向,
方向,![]() 位于
位于![]() 的正北方向,
的正北方向,![]() ,
,![]() 处一辆救护车欲通过道口前往
处一辆救护车欲通过道口前往![]() 处的医院送病人,发现北偏东
处的医院送病人,发现北偏东![]() 方向的
方向的![]() 处(火车头位置)有一列火车自东向西驶来,若火车通过每个道口都需要
处(火车头位置)有一列火车自东向西驶来,若火车通过每个道口都需要![]() 分钟,救护车和火车的速度均为
分钟,救护车和火车的速度均为![]() .
.
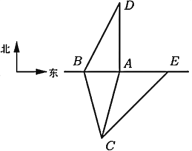
(1)判断救护车通过道口![]() 是否会受火车影响,并说明理由;
是否会受火车影响,并说明理由;
(2)为了尽快将病人送到医院,救护车应选择![]() 、
、![]() 中的哪个道口?通过计算说明.
中的哪个道口?通过计算说明.
查看答案和解析>>
科目:高中数学 来源: 题型:
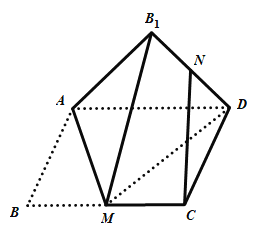
【题目】如图,矩形![]() 中,
中,![]() 为
为![]() 的中点,将
的中点,将![]() 沿直线
沿直线![]() 翻折成
翻折成![]() ,连结
,连结![]() ,
,![]() 为
为![]() 的中点,则在翻折过程中,下列说法中所有正确的是( )
的中点,则在翻折过程中,下列说法中所有正确的是( )
A.存在某个位置,使得![]()
B.翻折过程中,![]() 的长是定值
的长是定值
C.若![]() ,则
,则![]()
D.若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,三棱锥
的体积最大时,三棱锥![]() 的外接球的表面积是
的外接球的表面积是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某湿地公园的鸟瞰图是一个直角梯形,其中:![]() ,
,![]() ,
,![]() ,
,![]() 长1千米,
长1千米,![]() 长
长![]() 千米,公园内有一个形状是扇形的天然湖泊
千米,公园内有一个形状是扇形的天然湖泊![]() ,扇形
,扇形![]() 以
以![]() 长为半径,弧
长为半径,弧![]() 为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段
为湖岸,其余部分为滩地,B,D点是公园的进出口.公园管理方计划在进出口之间建造一条观光步行道:线段![]() 线段
线段![]() 弧
弧![]() ,其中Q在线段
,其中Q在线段![]() 上(异于线段端点),
上(异于线段端点),![]() 与弧
与弧![]() 相切于P点(异于弧端点]根据市场行情
相切于P点(异于弧端点]根据市场行情![]() ,
,![]() 段的建造费用是每千米10万元,湖岸段弧
段的建造费用是每千米10万元,湖岸段弧![]() 的建造费用是每千米
的建造费用是每千米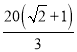 万元(步行道的宽度不计),设
万元(步行道的宽度不计),设![]() 为
为![]() 弧度观光步行道的建造费用为
弧度观光步行道的建造费用为![]() 万元.
万元.
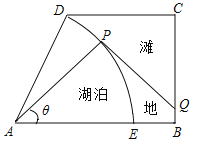
(1)求步行道的建造费用![]() 关于
关于![]() 的函数关系式,并求其走义域;
的函数关系式,并求其走义域;
(2)当![]() 为何值时,步行道的建造费用最低?
为何值时,步行道的建造费用最低?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=![]() ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.
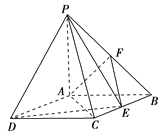
(1)点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(2)求证:无论点E在BC边的何处,都有![]() ;
;
(3)当![]() 为何值时,
为何值时,![]() 与平面
与平面![]() 所成角的大小为45°.
所成角的大小为45°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com