
【题目】已知椭圆 ![]() 的左,右焦点分别为F1 , F2 , 过F1任作一条与两坐标轴都不垂直的直线,与C交于A,B两点,且△ABF2的周长为8.当直线AB的斜率为
的左,右焦点分别为F1 , F2 , 过F1任作一条与两坐标轴都不垂直的直线,与C交于A,B两点,且△ABF2的周长为8.当直线AB的斜率为 ![]() 时,AF2与x轴垂直. (I)求椭圆C的方程;
时,AF2与x轴垂直. (I)求椭圆C的方程;
(Ⅱ)在x轴上是否存在定点M,总能使MF1平分∠AMB?说明理由.
【答案】解:(I)由椭圆的定义可知△ABF2的周长4a=8,则a=2,
由直线AB的斜率为 ![]() 时,AF2与x轴垂直,则tan∠AF1F2=
时,AF2与x轴垂直,则tan∠AF1F2= ![]() =
= ![]() =
= ![]() ,
,
则b2=3c,由b2=a2﹣c2=4﹣c2,
则b= ![]() ,c=1,
,c=1,
∴椭圆的标准方程为: ![]() ;
;
(Ⅱ)方法一:假设存在点(m,0),使MF1平分∠AMB,
由直线l的斜率显然存在,设直线l方程y=k(x+1),(k≠0),A(x1,y1),B(x2,y2),
由 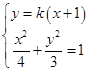 ,整理得:(3+4k2)x2+8k2x+4k2﹣12=1,
,整理得:(3+4k2)x2+8k2x+4k2﹣12=1,
∴x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
假设存在m,由x轴平分∠AMB可得,kMA+kMB=0,
即 ![]() +
+ ![]() =0,
=0,
k(x1+1)(x2﹣m)+k(x2+1)(x1﹣m)=0,
∴2x1x2﹣(m﹣1)(x1+x2)﹣2m=0,
∴8k2﹣24+8k2m﹣8k2﹣6m﹣8mk2=0,
解得:m=﹣4.
故存在点M(﹣4,0),使MF1平分∠AMB.
方法二:假设存在点(m,0),使MF1平分∠AMB,
由(I)可知:F1(﹣1,0),设直线AB为x=ty﹣1,(t≠0),A(x1,y1),B(x2,y2),
则 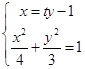 ,(3t2+4)y2﹣6ty﹣9=0,
,(3t2+4)y2﹣6ty﹣9=0,
则y1+y2= ![]() ,y1y2=﹣
,y1y2=﹣ ![]() ,
,
假设存在(m,0),由MF1平分∠AMB可得,kMA+kMB=0,
∴ ![]() +
+ ![]() =0,即y1(x1﹣m)+y2(x1﹣m)=0,
=0,即y1(x1﹣m)+y2(x1﹣m)=0,
即y1(ty2﹣1)+y2(ty1﹣1)﹣m(y1+y2)=0,
∴2ty1y2﹣(1+m)(y1+y2)=0,
2t×(﹣ ![]() )﹣(1﹣m)(
)﹣(1﹣m)( ![]() )=0,则1+m=﹣3,
)=0,则1+m=﹣3,
解得:m=﹣4,
故存在点M(﹣4,0),使MF1平分∠AMB
【解析】(I)由题意可知:4a=8,则a=2,由题意可知:tan∠AF1F2= ![]() =
= ![]() =
= ![]() ,即可求得b的值,求得椭圆方程;(Ⅱ)方法一:假设存在点(m,0),使MF1平分∠AMB,设直线l方程y=k(x+1),代入椭圆方程,利用韦达定理及直线的斜率公式可知:kMA+kMB=0,即可求得m的值;方法二:设直线AB为x=ty﹣1,代入椭圆方程,由韦达定理及直线的斜率公式可知:kMA+kMB=0,即可求得m的值.
,即可求得b的值,求得椭圆方程;(Ⅱ)方法一:假设存在点(m,0),使MF1平分∠AMB,设直线l方程y=k(x+1),代入椭圆方程,利用韦达定理及直线的斜率公式可知:kMA+kMB=0,即可求得m的值;方法二:设直线AB为x=ty﹣1,代入椭圆方程,由韦达定理及直线的斜率公式可知:kMA+kMB=0,即可求得m的值.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3﹣2ex2+mx﹣lnx,记g(x)= ![]() ,若函数g(x)至少存在一个零点,则实数m的取值范围是( )
,若函数g(x)至少存在一个零点,则实数m的取值范围是( )
A.(﹣∞,e2+ ![]() ]
]
B.(0,e2+ ![]() ]
]
C.(e2+ ![]() ,+∞]
,+∞]
D.(﹣e2﹣ ![]() ,e2+
,e2+ ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】春节来临,有农民工兄弟A、B、C、D四人各自通过互联网订购回家过年的火车票,若订票成功即可获得火车票,即他们获得火车票与否互不影响.若A、B、C、D获得火车票的概率分别是 ![]() ,其中p1>p3 , 又
,其中p1>p3 , 又 ![]() 成等比数列,且A、C两人恰好有一人获得火车票的概率是
成等比数列,且A、C两人恰好有一人获得火车票的概率是 ![]() .
.
(1)求p1 , p3的值;
(2)若C、D是一家人且两人都获得火车票才一起回家,否则两人都不回家.设X表示A、B、C、D能够回家过年的人数,求X的分布列和期望EX.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若不等式ln(x+2)+a(x2+x)≥0对于任意的x∈[﹣1,+∞)恒成立,则实数a的取值范围是( )
A.[0,+∞)
B.[0,1]
C.[0,e]
D.[﹣1,0]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班抽取20名学生周测物理考试成绩(单位:分)的频率分布直方图如下:
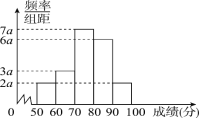
(1)求频率分布直方图中a的值,并写出众数;
(2)分别求出成绩落在[50,60)与[60,70)中的学生人数;
(3)从成绩在[50,70)的学生中任选2人,求这2人的成绩都在[60,70)中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的中心在原点O,左焦点为F1 , 圆O过点F1 , 且与双曲线的一个交点为P,若直线PF1的斜率为 ![]() ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.y=±x
B.y=± ![]() x
x
C.y=± ![]() x
x
D.y=± ![]() x
x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在(0,+∞)上的单调递减函数,f′(x)是其导函数,若 ![]() >x,则下列不等关系成立的是( )
>x,则下列不等关系成立的是( )
A.f(2)<2f(1)
B.3f(2)>2f(3)
C.ef(e)<f(e2)
D.ef(e2)>f(e3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com