
【题目】已知函数f(x)=alnx+ ![]() (a,b∈R)在点(1,f(1))处的切线方程为x﹣2y=0.
(a,b∈R)在点(1,f(1))处的切线方程为x﹣2y=0.
(1)求a,b的值;
(2)当x>1时,f(x)﹣kx<0恒成立,求实数k的取值范围;
(3)证明:当n∈N* , 且n≥2时, ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() .
.
【答案】
(1)解:f′(x)= ![]() ﹣
﹣ ![]() =
= ![]() ,f′(1)=a﹣
,f′(1)=a﹣ ![]() ,f(1)=
,f(1)= ![]() .
.
∵函数f(x)在点(1,f(1))处的切线方程为x﹣2y=0.
∴a﹣ ![]() =
= ![]() ,1﹣2×
,1﹣2× ![]() =0,解得b=2,a=1
=0,解得b=2,a=1
(2)解:f(x)=lnx+ ![]() .
.
当x>1时,f(x)﹣kx<0恒成立,
∴lnx+ ![]() ﹣kx<0,化为:k
﹣kx<0,化为:k ![]() +
+ ![]() =g(x).
=g(x).
g′(x)= ![]() ﹣
﹣ ![]() =
= ![]() .
.
令h(x)=x﹣xlnx﹣1,(x>1).
h′(x)=1﹣lnx﹣1=﹣lnx<0,
∴h(x)<h(1)=0,
∴g′(x)<0,∴函数g(x)在x∈(1,+∞)上单调递减.
∴k≥g(1)= ![]()
(3)证明:由(2)可知:x>1时, ![]() +
+ ![]() <
< ![]() ,化为
,化为 ![]() ,
,
令x=n≥2,则 ![]() >
> ![]() =
= ![]() .
.
∴当n∈N*,且n≥2时, ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() +
+ ![]()
= ![]() ﹣(
﹣( ![]() )=
)= ![]()
【解析】(1)f′(x)= ![]() ﹣
﹣ ![]() =
= ![]() ,f′(1)=a﹣
,f′(1)=a﹣ ![]() ,f(1)=
,f(1)= ![]() .由函数f(x)在点(1,f(1))处的切线方程为x﹣2y=0. 可得a﹣
.由函数f(x)在点(1,f(1))处的切线方程为x﹣2y=0. 可得a﹣ ![]() =
= ![]() ,1﹣2×
,1﹣2× ![]() =0,解得a,b.(2)f(x)=lnx+
=0,解得a,b.(2)f(x)=lnx+ ![]() .当x>1时,f(x)﹣kx<0恒成立,lnx+
.当x>1时,f(x)﹣kx<0恒成立,lnx+ ![]() ﹣kx<0,化为:k
﹣kx<0,化为:k ![]() +
+ ![]() =g(x).利用导数研究函数g(x)的单调性极值与最值即可得出.(3)由(2)可知:x>1时,
=g(x).利用导数研究函数g(x)的单调性极值与最值即可得出.(3)由(2)可知:x>1时, ![]() +
+ ![]() <
< ![]() ,化为
,化为 ![]() ,令x=n≥2,则
,令x=n≥2,则 ![]() >
> ![]() =
= ![]() .利用“累加求和”方法与“裂项求和”方法即可得出.
.利用“累加求和”方法与“裂项求和”方法即可得出.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,AC=BC= ![]() AA1 , D是棱AA1的中点,DC1⊥BD.
AA1 , D是棱AA1的中点,DC1⊥BD. 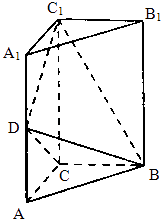
(1)证明:DC1⊥面BCD;
(2)设AA1=2,求点B1到平面BDC1的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中的一个椭圆,它的中心在原点,左焦点为 ![]() ,且过点D(2,0).
,且过点D(2,0).
(1)求该椭圆的标准方程;
(2)设点 ![]() ,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
,若P是椭圆上的动点,求线段PA的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( ).
A. ![]() ,“
,“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
B. “![]() 且
且![]() 为真命题”是“
为真命题”是“![]() 或
或![]() 为真命题” 的必要不充分条件
为真命题” 的必要不充分条件
C. 命题“![]() ,使得
,使得![]() ”的否定是:“
”的否定是:“![]() ”
”
D. 命题![]() :“
:“![]() ”,则
”,则![]() 是真命题
是真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】⊙O1和⊙O2的极坐标方程分别为ρ=4coθ,ρ=﹣sinθ.
(1)把⊙O1和⊙O2的极坐标方程化为直角坐标方程;
(2)求经过⊙O1 , ⊙O2交点的直线的极坐标方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com