
【题目】已知函数 f(x)=loga(x+1)﹣loga(1﹣x),a>0 且 a≠1.
(1)判断 f(x)的奇偶性并予以证明;
(2)当 a>1 时,求使 f(x)>0 的 x 的解集.
【答案】 (1)见解析(2) {x|0<x<1}.
【解析】分析:(1)先求出函数![]() 的定义域为
的定义域为![]() ,对任意
,对任意![]() ,求出
,求出![]() ,由此得到函数
,由此得到函数![]() 是奇函数;
是奇函数;
(2)由![]() 得
得![]() ,由此利用对数函数性质能求出不等式
,由此利用对数函数性质能求出不等式![]() 的解集.
的解集.
详解:(1)由题知![]() ,解得:﹣1<x<1,
,解得:﹣1<x<1,
∴函数 f(x)的定义域为(﹣1,1),f(x)是奇函数.
证明:∵函数 f(x)的定义域为(﹣1,1),所以对任意 x∈(﹣1,1),
f(﹣x)=loga(﹣x+1)﹣loga(1﹣(﹣x))=﹣[loga(x+1)﹣loga(1﹣x)]=﹣f(x),
所以函数 f(x)是奇函数.
(2)∵a>1,f(x)>0,∴loga(x+1)>loga(1﹣x),
∴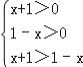 ,解得 0<x<1,
,解得 0<x<1,
所以不等式 f(x)>0 的解集为{x|0<x<1}.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如果定义在![]() 上的函数
上的函数![]() ,对任意的
,对任意的![]() ,都有
,都有![]() , 则称该函数是“
, 则称该函数是“![]() 函数”.
函数”.
(I)分别判断下列函数:①![]() ;②
;②![]() ; ③
; ③![]() ,是否为“
,是否为“![]() 函数”?(直接写出结论)
函数”?(直接写出结论)
(II)若函数![]() 是“
是“![]() 函数”,求实数
函数”,求实数![]() 的取值范围.
的取值范围.
(III)已知 是“
是“![]() 函数”,且在
函数”,且在![]() 上单调递增,求所有可能的集合
上单调递增,求所有可能的集合![]() 与
与![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC的内角A、B、C的对边分别为a、b、c,且满足sinA+sinB=[cosA﹣cos(π﹣B)]sinC.
(1)试判断△ABC的形状,并说明理由;
(2)若a+b+c=1+ ![]() ,试求△ABC面积的最大值.
,试求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
(Ⅰ)求该校报考飞行员的总人数;
(Ⅱ)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选三人,设X表示体重超过60公斤的学生人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知 f(x+1)=f(x﹣1),f(x)=f(﹣x+2),方程 f(x)=0 在[0,1]内有且只有一个 根 x=![]() ,则 f(x)=0 在区间[0,2016]内根的个数为( )
,则 f(x)=0 在区间[0,2016]内根的个数为( )
A. 2015 B. 1007 C. 2016 D. 1008
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C所对的边为a、b、c,且 ![]() asinC﹣c(2+cosA)=0.
asinC﹣c(2+cosA)=0.
(1)求角A的大小;
(2)若△ABC的最大边长为 ![]() ,且sinC=2sinB,求最小边长.
,且sinC=2sinB,求最小边长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1
(Ⅰ)设为P为AC的中点,Q为AB上一点,使PQ⊥OA,并计算 ![]() 的值;
的值;
(Ⅱ)求二面角O﹣AC﹣B的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】假设每一架飞机的每一个引擎在飞行中出现故障概率均为![]() ,且各引擎是否有故障是独立的,已知4引擎飞机中至少有3个引擎飞机正常运行,飞机就可成功飞行;2引擎飞机要2个引擎全部正常运行,飞机才可成功飞行.要使4引擎飞机比2引擎飞机更安全,则
,且各引擎是否有故障是独立的,已知4引擎飞机中至少有3个引擎飞机正常运行,飞机就可成功飞行;2引擎飞机要2个引擎全部正常运行,飞机才可成功飞行.要使4引擎飞机比2引擎飞机更安全,则![]() 的取值范围是__________.
的取值范围是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2|x+1|+|x﹣a|(a∈R).
(1)若 a=1,求不等式 f(x)≥5的解集;
(2)若函数f(x)的最小值为3,求实数 a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com