
【题目】(本小题共13分)根据以往的成绩记录,甲、乙两名队员射击击中目标靶的环数的频率分布情况如图所示
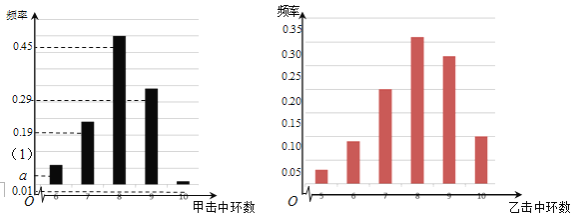
(1)求上图中![]() 的值;
的值;
(2)甲队员进行一次射击,求命中环数大于7环的概率(频率当作概率使用);
(3)由上图判断甲、乙两名队员中,哪一名队员的射击成绩更稳定(结论不需证明)
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,是否存在整数
时,是否存在整数![]() ,使不等式
,使不等式![]() 恒成立?若存在,求整数
恒成立?若存在,求整数![]() 的值;若不存在,则说明理由;
的值;若不存在,则说明理由;
(3)关于![]() 的方程
的方程![]() 在
在![]() 上恰有两个相异实根,求实数
上恰有两个相异实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ,
,![]() ,
,![]() ).
).
(1)若![]() 的部分图像如图所示,求
的部分图像如图所示,求![]() 的解析式;
的解析式;
(2)在(1)的条件下,求最小正实数![]() ,使得函数
,使得函数![]() 的图象向左平移
的图象向左平移![]() 个单位后所对应的函数是偶函数;
个单位后所对应的函数是偶函数;
(3)若![]() 在
在![]() 上是单调递增函数,求
上是单调递增函数,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为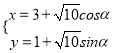 (
(![]() 为参数),以直角坐标系原点
为参数),以直角坐标系原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 的极坐标方程,并说明其表示什么轨迹;
的极坐标方程,并说明其表示什么轨迹;
(2)若直线的极坐标方程为![]() ,求直线被曲线
,求直线被曲线![]() 截得的弦长.
截得的弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱柱ABC-A1B1C1中,侧棱垂直于底面,AC=BC,点D是AB的中点.

(1)求证:BC1∥平面CA1D;(2)若底面ABC为边长为2的正三角形,BB1=![]() 求三棱锥B1-A1DC的体积.
求三棱锥B1-A1DC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某棋类游戏的规则如下:棋子的初始位置在起点处,玩家每掷出一枚骰子,朝上一面的点数即为向终点方向前进的格子数,(比如玩家一开始掷出的骰子点数为3,则走到炸弹所在位置),若踩到炸弹则返回起点重新开始,若达到终点则游戏结束.现在已知小明掷完三次骰子后游戏恰好结束,则所有不同的情况种数为__________.
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校大一新生中的6名同学打算参加学校组织的“雅荷文学社”、“青春风街舞社”、“羽乒协会”、“演讲团”、“吉他协会”五个社团,若每名同学必须参加且只能参加1个社团且每个社团至多两人参加,则这6个人中至多有1人参加“演讲团”的不同参加方法数为( )
A. 4680 B. 4770 C. 5040 D. 5200
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com