Question

【题目】设是20个两两不同的正整数，且集合中有201个不同的元素.求集合中不同元素个数的最小可能值.

Answer 1

【答案】100

【解析】

所给集合的元素个数的最小值为100.

例子：令，

.

则中共有个不同的元素.

而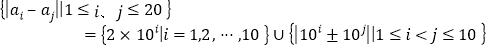

共有个不同的元素.

下面证明：所给集合的不同元素的个数不小于100.

用反证法证明.

若存在一个使所给集合的元素个数小于100的集合.计算的“好子集”的个数，这里，，且.

对中满足的数对（共190对），考虑它们的差，由假设知至多有99个不同的差，故必有至少91个数对，使得存在，满足，，且.对这样的91个数对，它与其对应的、形成的一个四元集，可以得到的一个好子集，且至多两个数对形成相同的子集（只能是或）.故S的好子集至少有46个.

另一方面，的好子集的个数等于，这里，为中满足，的数对的个数.

注意到，对每个，中的每个元素至多出现在上面的一个数对中（事实上，当时，出现在数对中，其余情况出现在中），于是，.从而，在时，.故.

由于集合中有201个不同的元素，故使得的正整数有201个.设为这样的组成的集合，利用中有对满足，有20对满足，故.

则.

这与前面所得到的结论：的好子集至少有46个矛盾.

因此，所给的集合中，至少有100个不同的元素.