
【题目】设椭圆![]() =1(a>b>0)的左、右焦点分别为F1,F2,P是椭圆上一点,|PF1|=λ|PF2|
=1(a>b>0)的左、右焦点分别为F1,F2,P是椭圆上一点,|PF1|=λ|PF2|![]() ,∠F1PF2=
,∠F1PF2=![]() ,则椭圆离心率的取值范围为( )
,则椭圆离心率的取值范围为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】购买一件售价为5 000元的商品,采用分期付款的办法,每期付款数相同,购买后1个月付款一次,过1个月再付款一次,如此下去,到第12次付款后全部付清.如果月利率为0.8%,每月利息按复利计算(上月利息计入下月本金),那么每期应付款多少元?(精确到1元)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 为椭圆
为椭圆![]() 的左顶点,点
的左顶点,点![]() 为椭圆
为椭圆![]() 的上顶点,且
的上顶点,且![]() .
.
(1)若椭圆![]() 的离心率为
的离心率为![]() ,求椭圆
,求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上一点,且在第一象限内,直线
上一点,且在第一象限内,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,若以
,若以![]() 为直径的圆经过点
为直径的圆经过点![]() ,证明:点
,证明:点![]() 在直线
在直线![]() 上.
上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=10n﹣n2(n∈N*),又bn=|an|(n∈N*).
(1)求数列{an}的通项公式;
(2)求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通部门对某路段公路上行驶的汽车速度实施监控,从速度在50﹣90km/h的汽车中抽取150辆进行分析,得到数据的频率分布直方图如图所示,则速度在70km/h以下的汽车有辆.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,已知椭圆C: ![]() =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ![]() ,左顶点为A(﹣4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
,左顶点为A(﹣4,0),过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E. 
(1)求椭圆C的方程;
(2)已知P为AD的中点,是否存在定点Q,对于任意的k(k≠0)都有OP⊥EQ,若存在,求出点Q的坐标;若不存在说明理由;
(3)若过O点作直线l的平行线交椭圆C于点M,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】朱世杰是历史上最伟大的数学家之一,他所著的《四元玉鉴》卷中“如像招数”五问中有如下问题:“今有官司差夫一千八百六十四人筑堤,只云初日差六十四人,次日转多七人,每人日支米三升”。其大意为“官府陆续派遣1864人前往修筑堤坝,第一天派出64人,从第二天开始每天派出的人数比前一天多7人,修筑堤坝的每人每天分发大米3升”,在该问题中第3天共分发大米( )
A. 192升 B. 213升 C. 234升 D. 255升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知AB为半圆O的直径,AB=4,C为半圆上一点,过点C作半圆的切线CD,过点A作AD⊥CD于D,交半圆于点E,DE=1.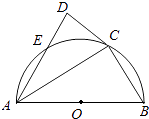
(1)求证:AC平分∠BAD;
(2)求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com