
【题目】正三棱柱ABC﹣A1B1C1底面△ABC的边长为3,此三棱柱的外接球的半径为 ![]() ,则异面直线AB1与BC1所成角的余弦值为 .
,则异面直线AB1与BC1所成角的余弦值为 .
【答案】![]()
【解析】解:设三棱柱外接球的球心为O,球半径为r, 三棱柱的底面三角形ABC的中心为D,如图,
∵正三棱柱ABC﹣A1B1C1底面△ABC的边长为3,此三棱柱的外接球的半径为 ![]() ,
,
∴OA= ![]() ,AD=
,AD= ![]() =
= ![]() ,
,
∴OD= ![]() =2,∴AA1=4,
=2,∴AA1=4,
以A为原点,以过A在平面ABC中作AC的垂线为x轴,以AC为y轴,AA1为z轴,
建立空间直角坐标系,
A(0,0,0),B( ![]() ,
, ![]() ,0),
,0),
B1( ![]() ,
, ![]() ,4),C1(0,3,4),
,4),C1(0,3,4),![]() =(
=( ![]() ,
, ![]() ,4),
,4), ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,4),
,4),
设异面直线AB1与BC1所成角为θ,
则cosθ=  =
= ![]() =
= ![]() .
.
∴异面直线AB1与BC1所成角的余弦值为 ![]() .
.
所以答案是: ![]() .
.
【考点精析】掌握异面直线及其所成的角是解答本题的根本,需要知道异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线的顶点在原点,过点A(-4,4)且焦点在x轴.
(1)求抛物线方程;
(2)直线l过定点B(-1,0)与该抛物线相交所得弦长为8,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】等差数列{an}的前n项和为Sn , 已知a2=7,a3为整数,且Sn的最大值为S5 .
(1)求{an}的通项公式;
(2)设bn= ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知美国苹果公司生产某款iphone手机的年固定成本为40万美元,每生产1只还需另投入16美元.设苹果公司一年内共生产该款iphone手机x万只并全部销售完,每万只的销售收入为R(x)万美元,且R(x)= 
(1)写出年利润W(万元)关于年产量x(万只)的函数解析式;
(2)当年产量为多少万只时,苹果公司在该款手机的生产中所获得的利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() 的半径为2,圆心在
的半径为2,圆心在![]() 轴的正半轴上,且与直线
轴的正半轴上,且与直线![]() 相切.
相切.
(1)求圆![]() 的方程。
的方程。
(2)在圆![]() 上,是否存在点
上,是否存在点![]() ,使得直线
,使得直线![]() 与圆
与圆![]() 相交于不同的两点
相交于不同的两点![]() ,且△
,且△![]() 的面积最大?若存在,求出点
的面积最大?若存在,求出点![]() 的坐标及对应的△
的坐标及对应的△![]() 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是2017年第一季度五省GDP情况图,则下列陈述中不正确的是( )
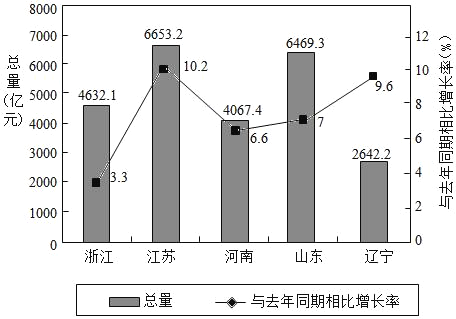
A. 2017年第一季度![]() 总量和增速由高到低排位均居同一位的省只有1个
总量和增速由高到低排位均居同一位的省只有1个
B. 与去年同期相比,2017年第一季度五个省的![]() 总量均实现了增长
总量均实现了增长
C. 去年同期河南省的![]() 总量不超过4000亿元
总量不超过4000亿元
D. 2017年第一季度![]() 增速由高到低排位第5的是浙江省
增速由高到低排位第5的是浙江省
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个命题中:①“等边三角形的三个内角均为60°”的逆命题;
②“若![]() ,则方程
,则方程![]() 有实根”的逆否命题;
有实根”的逆否命题;
③“全等三角形的面积相等”的否命题;
④“若![]() ,则
,则![]() ”的否命题.
”的否命题.
其中真命题的个数是( )
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x﹣a,g(x)=x+2.
(1)当a=1时,求不等式f(x)+f(﹣x)≤g(x)的解集;
(2)求证: ![]() 中至少有一个不小于
中至少有一个不小于 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com