
【题目】如图,在直四棱柱ABCD—A1B1C1D1中,AB=BD=1,![]() ,AA1=BC=2,AD∥BC.
,AA1=BC=2,AD∥BC.

(1)证明:BD⊥平面ABB1A1.
(2)比较四棱锥D—ABB1A1与四棱锥D—A1B1C1D1的体积的大小.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=1和定点A(2,1),由圆O外一点P(a,b)向圆O引切线PQ,切点为Q,|PQ|=|PA|成立,如图.
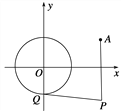
(1)求a,b间的关系;
(2)求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某项娱乐活动的海选过程中评分人员需对同批次的选手进行考核并评分,并将其得分作为该选手的成绩,成绩大于等于![]() 分的选手定为合格选手,直接参加第二轮比赛,大于等于
分的选手定为合格选手,直接参加第二轮比赛,大于等于![]() 分的选手将直接参加竞赛选拔赛.已知成绩合格的
分的选手将直接参加竞赛选拔赛.已知成绩合格的![]() 名参赛选手成绩的频率分布直方图如图所示,其中
名参赛选手成绩的频率分布直方图如图所示,其中![]() 的频率构成等比数列.
的频率构成等比数列.
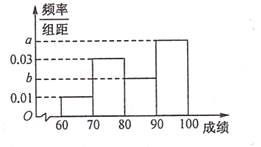
(1)求![]() 的值;
的值;
(2)估计这![]() 名参赛选手的平均成绩;
名参赛选手的平均成绩;
(3)根据已有的经验,参加竞赛选拔赛的选手能够进入正式竞赛比赛的概率为![]() ,假设每名选手能否通过竞赛选拔赛相互独立,现有
,假设每名选手能否通过竞赛选拔赛相互独立,现有![]() 名选手进入竞赛选拔赛,记这
名选手进入竞赛选拔赛,记这![]() 名选手在竞赛选拔赛中通过的人数为随机变量
名选手在竞赛选拔赛中通过的人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强学生体质,合肥一中组织体育社团,某班级有4人积极报名参加篮球和足球社团,每人只能从两个社团中选择其中一个社团,大家约定:每个人通过掷一枚质地均匀的骰子决定自己参加哪个社团,掷出点数为5或6的人参加篮球社团,掷出点数小于5的人参加足球社团.
(1)求这4人中恰有1人参加篮球社团的概率;
(2)用![]() ,
,![]() 分别表示这4人中参加篮球社团和足球社团的人数,记随机变量X为
分别表示这4人中参加篮球社团和足球社团的人数,记随机变量X为![]() 和
和![]() 之差的绝对值,求随机变量X的分布列与数学期望
之差的绝对值,求随机变量X的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD的底面是矩形,PA⊥平面ABCD,E,F分别是AB,PD的中点,且PA=AD.

(Ⅰ)求证:AF∥平面PEC;
(Ⅱ)求证:平面PEC⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
②设有一个回归方程![]() ,变量
,变量![]() 增加1个单位时,
增加1个单位时,![]() 平均增加5个单位
平均增加5个单位
③线性回归方程![]() 必过
必过![]()
④设具有相关关系的两个变量![]() 的相关系数为
的相关系数为![]() ,那么
,那么![]() 越接近于0,
越接近于0,![]() 之间的线性相关程度越高;
之间的线性相关程度越高;
⑤在一个![]() 列联表中,由计算得
列联表中,由计算得![]() 的值,那么
的值,那么![]() 的值越大,判断两个变量间有关联的把握就越大。
的值越大,判断两个变量间有关联的把握就越大。
其中错误的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知函数![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 的图象与
的图象与![]() 轴、
轴、![]() 轴的交点,
轴的交点,![]() 、
、![]() 分别是
分别是![]() 的图象上横坐标为
的图象上横坐标为![]() 、
、![]() 的两点,
的两点,![]() 轴,且
轴,且![]() 、
、![]() 、
、![]() 三点共线.
三点共线.

(1)求函数![]() 的解析式;
的解析式;
(2)若![]() ,
,![]() ,求
,求![]() ;
;
(3)若关于![]() 的函数
的函数![]() 在区间
在区间![]() 上恰好有一个零点,求实数
上恰好有一个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com