
【题目】【2017届河北省正定中学高三上学期第三次月考(期中)数学(理)】在平面直角坐标系中,当![]() 不是原点时,定义
不是原点时,定义![]() 的“伴随点”为
的“伴随点”为![]() ;当
;当![]() 是原点时,定义
是原点时,定义![]() 的“伴随点”为它自身,平面曲线
的“伴随点”为它自身,平面曲线![]() 上所有点的“伴随点”所构成的曲线
上所有点的“伴随点”所构成的曲线![]() 定义为曲线
定义为曲线![]() 的“伴随曲线”,现有下列命题:
的“伴随曲线”,现有下列命题:
①若点![]() 的“伴随点”是点
的“伴随点”是点![]() ,则点
,则点![]() 的“伴随点”是点
的“伴随点”是点![]() ;
;
②若曲线![]() 关于
关于![]() 轴对称,则其“伴随曲线”
轴对称,则其“伴随曲线” ![]() 关于
关于![]() 轴对称;
轴对称;
③单位圆的“伴随曲线”是它自身;
④一条直线的“伴随曲线”是一条直线.
其中真命题的个数为( )
A. 1 B. 2 C. 3 D. 4
科目:高中数学 来源: 题型:
【题目】性格色彩学创始人乐嘉是江苏电视台当红节目“非诚勿扰”的特约嘉宾,他的点评视角独特,语言犀利,给观众留下了深刻的印象,某报社为了了解观众对乐嘉的喜爱程度,随机调查了观看了该节目的140名观众,得到如下的列联表:(单位:名)
男 | 女 | 总计 | ||||||
喜爱 | 40 | 60 | 100 | |||||
不喜爱 | 20 | 20 | 40 | |||||
总计 | 60 | 80 | 140 | |||||
p(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | |||
k0 | 2.705 | 3.841 | 5.024 | 6.635 | 7.879 | |||
(Ⅰ)从这60名男观众中按对乐嘉是否喜爱采取分层抽样,抽取一个容量为6的样本,问样本中喜爱与不喜爱的观众各有多少名?
(Ⅱ)根据以上列联表,问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱乐嘉有关?(精确到0.001)
(Ⅲ)从(Ⅰ)中的6名男性观众中随机选取两名作跟踪调查,求选到的两名观众都喜爱乐嘉的概率.
附: 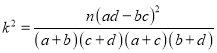
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)若![]() 和
和![]() 在区间
在区间![]() 内具有相同的单调性,求实数
内具有相同的单调性,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() ,且函数
,且函数![]() 的最小值为
的最小值为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为R的函数![]() 是奇函数
是奇函数
(1)求![]() 的值
的值
(2)判断f(x)在![]() 上的单调性。(直接写出答案,不用证明)
上的单调性。(直接写出答案,不用证明)
(3)若对于任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考四川文科】已知数列{![]() }的首项为1,
}的首项为1,![]() 为数列
为数列![]() 的前n项和,
的前n项和,![]() ,其中q>0,
,其中q>0,![]() .
.
(Ⅰ)若![]() 成等差数列,求
成等差数列,求![]() 的通项公式;
的通项公式;
(Ⅱ)设双曲线![]() 的离心率为
的离心率为![]() ,且
,且![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】罗源滨海新城建一座桥,两端的桥墩已建好,这两墩相距![]() 米,余下工程只需建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为32万元,距离为x米的相邻两墩之间的桥面工程费用为
米,余下工程只需建两端桥墩之间的桥面和桥墩,经预测,一个桥墩的工程费用为32万元,距离为x米的相邻两墩之间的桥面工程费用为![]() 万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为
万元.假设桥墩等距离分布,所有桥墩都视为点,且不考虑其他因素,记余下工程的费用为![]() 万元.
万元.
(1)试写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)当![]() =96米,需新建多少个桥墩才能使余下工程的费用
=96米,需新建多少个桥墩才能使余下工程的费用![]() 最小?
最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在区间
在区间![]() 上为单调递增函数,求
上为单调递增函数,求![]() 的取值范围;
的取值范围;
(3)当![]() 时,函数
时,函数![]() 的图象与
的图象与![]() 轴交于两点
轴交于两点![]() 且
且![]() ,又
,又![]() 是
是![]() 的导函数.若正常数
的导函数.若正常数![]() 满足条件
满足条件![]() .证明:
.证明: ![]() <0.
<0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com