
【题目】已知函数![]() 是定义在
是定义在![]() 上的奇函数,对于任意
上的奇函数,对于任意![]() ,
,![]() ,
,![]() 总有
总有![]() 且
且![]() .若对于任意
.若对于任意![]() ,存在
,存在![]() ,使
,使![]() 成立,则实数
成立,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() 或
或![]()
C. ![]() 或
或![]() D.
D. ![]() 或
或![]() 或
或![]()
【答案】D
【解析】
由条件先判断函数的单调性,利用奇偶性和单调性的性质将不等式转化f(x)min≤t2﹣2at﹣1成立,构造函数g(a)即可得到结论.
∵f(x)是定义在[﹣1,1]上的奇函数,
∴当x1、x2∈[﹣1,1],且x1+x2≠0时,有![]() 0,
0,
∴函数f(x)在[﹣1,1]上单调递增.
∵f(1)=1,
∴f(x)的最小值为f(﹣1)=﹣f(1)=﹣1,最大值为f(1)=1,
若对于任意a∈[﹣1,1],存在x∈[﹣1,1],使f(x)≤t2﹣2at﹣1成立,
即t2﹣2at﹣1≥﹣1对所有a∈[﹣1,1]恒成立,
∴t2﹣2at≥0,
设g(a)=t2﹣2at=﹣2ta+t2,
则满足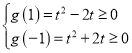 ,
,
即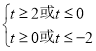 ,
,
∴t≥2或t≤﹣2或t=0,
故选:D.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax﹣cosx,a≠0.
(1)若函数f(x)为单调函数,求a的取值范围;
(2)若x∈[0,2π],求:当a≥![]() 时,函数f(x)仅有一个零点.
时,函数f(x)仅有一个零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义首项为1且公比为正数的等比数列为“M-数列”.
(1)已知等比数列{an}满足:![]() ,求证:数列{an}为“M-数列”;
,求证:数列{an}为“M-数列”;
(2)已知数列{bn}满足:![]() ,其中Sn为数列{bn}的前n项和.
,其中Sn为数列{bn}的前n项和.
①求数列{bn}的通项公式;
②设m为正整数,若存在“M-数列”{cn}![]() ,对任意正整数k,当k≤m时,都有
,对任意正整数k,当k≤m时,都有![]() 成立,求m的最大值.
成立,求m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下说法正确的是( )
A.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
B.命题“![]() ,
,![]() 互为倒数,则
互为倒数,则![]() ”的逆命题为真
”的逆命题为真
C.命题“若![]() ,
,![]() 都是偶数,则
都是偶数,则![]() 是偶数”的否命题为真
是偶数”的否命题为真
D.“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两队进行防溺水专题知识竞赛,每队3人,首轮比赛每人一道必答题,答对者则为本队得1分,答错或不答得0分,己知甲队每人答对的概率分别为![]() ,
,![]() ,
,![]() ,乙队每人答对的概率均为
,乙队每人答对的概率均为![]() .设每人回答正确与否互不影响,用
.设每人回答正确与否互不影响,用![]() 表示首轮比赛结束后甲队的总得分.
表示首轮比赛结束后甲队的总得分.
(1)求随机变量![]() 的分布列;
的分布列;
(2)求在首轮比赛结束后甲队和乙队得分之和为2的条件下,甲队比乙队得分高的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com