
【题目】在△ABC中,角A、B、C所对的边分别为a、b、c,且![]()
(1)判断△ABC的形状,并加以证明;
(2)当c = 1时,求△ABC周长的最大值.
【答案】(1)见解析;(2)ABC周长的最大值为 ![]()
.
【解析】试题分析:(1)由![]() 可得:
可得: ![]() 即cosA=
即cosA=![]() ,即b=c×cosA
,即b=c×cosA
由余弦定理得: ![]() ∴c2=a2+b2即得三角形形状(2)由(1)知△ABC为直角三角形,c为斜边,当c=1时设另两直角边长分别为a,b,则a2+b2=1 ∵
∴c2=a2+b2即得三角形形状(2)由(1)知△ABC为直角三角形,c为斜边,当c=1时设另两直角边长分别为a,b,则a2+b2=1 ∵![]() ∴△ABC周长=1+a+b
∴△ABC周长=1+a+b![]() 即得△ABC周长的最大值.
即得△ABC周长的最大值.
试题解析:
(1)原式可得: ![]()
即cosA=![]() 即b=c×cosA
即b=c×cosA
由余弦定理得: ![]()
∴c2=a2+b2 即△ABC为直角三角形
(2)由(1)知△ABC为直角三角形,c为斜边
当c=1时设另两直角边长分别为a,b
a2+b2=1
∵![]()
∴△ABC周长=1+a+b![]()
当且仅当a=b即 △ABC为等腰直角三角形时取等号.
∴△ABC周长的最大值为 ![]()


科目:高中数学 来源: 题型:
【题目】已知在直角坐标系xOy中,曲线C1的参数方程为 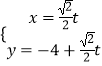 (t为参数),在极坐标系(以坐标原点O为极点,x轴的正半轴为极轴)中,曲线C2的方程为ρsin2θ=2pcosθ(p>0),曲线C1、C2交于A、B两点.
(t为参数),在极坐标系(以坐标原点O为极点,x轴的正半轴为极轴)中,曲线C2的方程为ρsin2θ=2pcosθ(p>0),曲线C1、C2交于A、B两点.
(Ⅰ)若p=2且定点P(0,﹣4),求|PA|+|PB|的值;
(Ⅱ)若|PA|,|AB|,|PB|成等比数列,求p的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】提高过江大桥的车辆通行的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度![]() (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度![]() (单位:辆/千米)
(单位:辆/千米)
的函数.当桥上的车流密度达到200辆/千米时,就会造成堵塞,此时车流速度为0;当
车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当![]() 时,
时,
车流速度![]() 是车流密度
是车流密度![]() 的一次函数.
的一次函数.
(1)当![]() 时,求函数
时,求函数![]() 的表达式;
的表达式;
(2)如果车流量(单位时间内通过桥上某观测点的车辆数)![]() (单位:辆/小时),那么当车流密度
(单位:辆/小时),那么当车流密度![]() 为多大时,车流量
为多大时,车流量![]() 可以达到最大,并求出最大值.(精确到
可以达到最大,并求出最大值.(精确到![]() 辆/小时).
辆/小时).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且满足a1=1,nSn+1﹣(n+1)Sn= ![]() ,n∈N*
,n∈N*
(1)求a2的值;
(2)求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两个篮球运动员互不影响地在同一位置投球,命中率分别为 ![]() 与p,且乙投球2次均未命中的概率为
与p,且乙投球2次均未命中的概率为 ![]() .
.
(Ⅰ)求乙投球的命中率p;
(Ⅱ)若甲投球1次,乙投球2次,两人共命中的次数记为ξ,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某农场共有土地50亩,这些地可种西瓜、棉花、玉米.这些农作物每亩地所需劳力和预计产值如下表.若该农场有20名劳动力,应怎样计划才能使每亩地都能种上作物(玉米必种),所有劳动力都被安排工作(每名劳动力只能种植一种作物)且作物预计总产值达最高?
作物 | 劳力/亩 | 产值/亩 |
西瓜 | 1/2 | 0.6万元 |
棉花 | 1/3 | 0.5万元 |
玉米 | 1/4 | 0.3万元 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C的对边分别为a、b、c,已知2cos(B﹣C)﹣1=4cosBcosC.
(1)求A;
(2)若a= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求b+c.
,求b+c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“累积净化量(CCM)”是空气净化器质量的一个重要衡量指标,它是指空气净化器从开始使用到净化效率为50%时对颗粒物的累积净化量,以克表示.根据GB/T18801﹣2015《空气净化器》国家标准,对空气净化器的累积净化量(CCM)有如下等级划分:
累积净化量(克) | (3,5] | (5,8] | (8,12] | 12以上 |
等级 | P1 | P2 | P3 | P4 |
为了了解一批空气净化器(共2000台)的质量,随机抽取n台机器作为样本进行估计,已知这n台机器的
累积净化量都分布在区间(4,14]中,按照(4,6],(6,8],(8,10],(10,12],(12,14],均匀分组,其中累积净化量在(4,6]的所有数据有:4.5,4.6,5.2,5.7和5.9,并绘制了如下频率分布直方图.
(Ⅰ)求n的值及频率分布直方图中的x值;
(Ⅱ)以样本估计总体,试估计这批空气净化器(共2000台)中等级为P2的空气净化器有多少台?
(Ⅲ)从累积净化量在(4,6]的样本中随机抽取2台,求恰好有1台等级为P2的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com