
【题目】定义在[0,+∞)上的函数f(x)满足:①当x∈[1,2)时, ![]() ;②x∈[0,+∞)都有f(2x)=2f(x).设关于x的函数F(x)=f(x)﹣a的零点从小到大依次为x1 , x2 , x3 , …xn , …,若
;②x∈[0,+∞)都有f(2x)=2f(x).设关于x的函数F(x)=f(x)﹣a的零点从小到大依次为x1 , x2 , x3 , …xn , …,若 ![]() ,则x1+x2+…+x2n= .
,则x1+x2+…+x2n= .
【答案】6×(2n﹣1)
【解析】解:∵①当x∈[1,2)时, ![]() ;②x∈[0,+∞)都有f(2x)=2f(x). 当x∈[2,4)时,
;②x∈[0,+∞)都有f(2x)=2f(x). 当x∈[2,4)时, ![]() ∈[1,2),
∈[1,2),
f(x)=2f( ![]() x)=2(
x)=2( ![]() ﹣|
﹣| ![]() ﹣
﹣ ![]() |)=1﹣|x﹣3|,x∈[4,8)时,
|)=1﹣|x﹣3|,x∈[4,8)时, ![]() ∈[2,4),
∈[2,4), 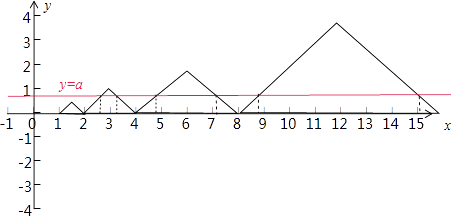
f(x)=2f( ![]() x)=2(1﹣|
x)=2(1﹣| ![]() x﹣3|)=2﹣|x﹣6|,
x﹣3|)=2﹣|x﹣6|,
同理,则 ![]() ,F(x)=f(x)﹣a在区间(2,3)和(3,4)上各有1个零点,分别为x1 , x2 , 且满足x1+x2=2×3=6,
,F(x)=f(x)﹣a在区间(2,3)和(3,4)上各有1个零点,分别为x1 , x2 , 且满足x1+x2=2×3=6,
依此类推:x3+x4=2×6=12,x5+x6=2×12=24…,x2n﹣1+x2n=2×3×2n﹣1 .
∴当 ![]() 时,x1+x2+…+x2n﹣1+x2n=6×(1+2+22+…+2n﹣1)=6×
时,x1+x2+…+x2n﹣1+x2n=6×(1+2+22+…+2n﹣1)=6× ![]() =6×(2n﹣1),
=6×(2n﹣1),
所以答案是:6×(2n﹣1).


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 和
和![]() 是函数
是函数![]() 的图象与
的图象与![]() 轴的
轴的![]() 个相邻交点的横坐标,且当
个相邻交点的横坐标,且当![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.
(1)求数![]() 的表达式;
的表达式;
(2)将函数![]() 的图象上的每一点的横坐标变为原来的
的图象上的每一点的横坐标变为原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象,再将函数
的图象,再将函数![]() 的图象向右平移
的图象向右平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象.
的图象.
①求函数![]() 的解析式;
的解析式;
②求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某公司为郑州园博园生产某特许商品,该公司年固定成本为10万元,每生产千件需另投入2 .7万元,设该公司年内共生产该特许商品工x千件并全部销售完;每千件的销售收入为R(x)万元,
且 ,
,
(I)写出年利润W(万元〉关于该特许商品x(千件)的函数解析式;
〔II〕年产量为多少千件时,该公司在该特许商品的生产中所获年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知2bcosC=acosC+ccosA.
(1)求角C的大小;
(2)若b=2,c=![]() ,求a及△ABC的面积.
,求a及△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:如果函数f(x)在[a,b]上存在x1 , x2(a<x1<x2<b)满足 ![]() ,
, ![]() 则称函数f(x)是[a,b]上的“中值函数”.已知函数
则称函数f(x)是[a,b]上的“中值函数”.已知函数 ![]() 是[0,m]上的“中值函数”,则实数m的取值范围是( )
是[0,m]上的“中值函数”,则实数m的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() ,以原点为极点,
,以原点为极点,![]() 轴正半轴为极轴建立极坐标系,圆
轴正半轴为极轴建立极坐标系,圆![]() 极坐标方程为
极坐标方程为![]() .
.
(1)若直线![]() 与圆
与圆![]() 相切,求
相切,求![]() 的值;
的值;
(2)已知直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() 两点,记点
两点,记点![]() 、
、![]() 相应的参数分别为
相应的参数分别为![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1: ![]() (a>b>0)的离心率为
(a>b>0)的离心率为 ![]() ,P(﹣2,1)是C1上一点.
,P(﹣2,1)是C1上一点.
(1)求椭圆C1的方程;
(2)设A,B,Q是P分别关于两坐标轴及坐标原点的对称点,平行于AB的直线l交C1于异于P、Q的两点C,D,点C关于原点的对称点为E.证明:直线PD、PE与y轴围成的三角形是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com