
【题目】已知A、B、C是椭圆W:![]() 上的三个点,O是坐标原点.
上的三个点,O是坐标原点.
(I)当点B是W的右顶点,且四边形OABC为菱形时,求此菱形的面积.
(II)当点B不是W的顶点时,判断四边形OABC是否可能为菱形,并说明理由.
【答案】(I)![]() (II) 不可能是菱形
(II) 不可能是菱形
【解析】
解:(1)椭圆W:![]() +y2=1的右顶点B的坐标为(2,0).
+y2=1的右顶点B的坐标为(2,0).
因为四边形OABC为菱形,所以AC与OB相互垂直平分.
所以可设A(1,m),
代入椭圆方程得![]() +m2=1,即m=±
+m2=1,即m=±![]() .
.
所以菱形OABC的面积是
![]() |OB|·|AC|=
|OB|·|AC|=![]() ×2×2|m|=
×2×2|m|=![]() .
.
(2)四边形OABC不可能为菱形.理由如下:
假设四边形OABC为菱形.
因为点B不是W的顶点,且直线AC不过原点,
所以可设AC的方程为y=kx+m(k≠0,m≠0).
由![]()
消y并整理得(1+4k2)x2+8kmx+4m2-4=0.
设A(x1,y1),C(x2,y2),则![]() =-
=-![]() ,
,![]() =k·
=k·![]() +m=
+m=![]() .
.
所以AC的中点为M![]() .
.
因为M为AC和OB的交点,
所以直线OB的斜率为-![]() .
.
因为k·![]() ≠-1,所以AC与OB不垂直.
≠-1,所以AC与OB不垂直.
所以四边形OABC不是菱形,与假设矛盾.
所以当点B不是W的顶点时,四边形OABC不可能是菱形.


科目:高中数学 来源: 题型:
【题目】如图,![]() 是圆
是圆![]() 的直径,点
的直径,点![]() 是圆
是圆![]() 上异于
上异于![]() ,
,![]() 的点,直线
的点,直线![]() 平面
平面![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
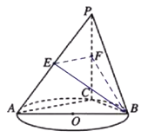
(Ⅰ)记平面![]() 与平面
与平面![]() 的交线为
的交线为![]() ,试判断直线
,试判断直线![]() 与平面
与平面![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(Ⅱ)设![]() ,求二面角
,求二面角![]() 大小的取值范围.
大小的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() =1(a>b>0),定义椭圆C上的点M(x0,y0)的“伴随点”为
=1(a>b>0),定义椭圆C上的点M(x0,y0)的“伴随点”为![]() .
.
(1)求椭圆C上的点M的“伴随点”N的轨迹方程;
(2)如果椭圆C上的点(1,![]() )的“伴随点”为(
)的“伴随点”为(![]() ,
,![]() ),对于椭圆C上的任意点M及它的“伴随点”N,求
),对于椭圆C上的任意点M及它的“伴随点”N,求![]() 的取值范围;
的取值范围;
(3)当a=2,b=![]() 时,直线l交椭圆C于A,B两点,若点A,B的“伴随点”分别是P,Q,且以PQ为直径的圆经过坐标原点O,求△OAB的面积.
时,直线l交椭圆C于A,B两点,若点A,B的“伴随点”分别是P,Q,且以PQ为直径的圆经过坐标原点O,求△OAB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,下列命题:
,下列命题:
①![]() 既不是奇函数,也不是偶函数
既不是奇函数,也不是偶函数
②若![]() 是三角形的内角,则
是三角形的内角,则![]() 是增函数
是增函数
③若![]() 是三角形的内角, 则
是三角形的内角, 则![]() 有最大值而无最小值
有最大值而无最小值
④![]() 的最小正周期是
的最小正周期是![]()
其中真命题的序号是( )
A.①②B.①③C.②③D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不垂直的是![]()
![]()
A. 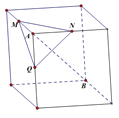 B.
B. 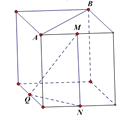
C. 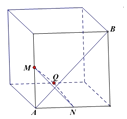 D.
D. 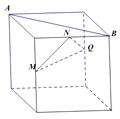
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com