
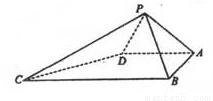
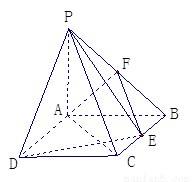
如图,四棱锥 中,
中,

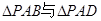 都是边长为
都是边长为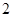 的等边三角形.
的等边三角形.
(I)证明: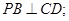
(II)求点A到平面PCD的距离.
(I)见解析(II)1
【解析】(Ⅰ)证明:取BC的中点E,连结DE,则ABED为正方形.
过P作PO⊥平面ABCD,垂足为O.
连结OA,OB,OD,OE.
由 和
和 都是等边三角形知PA=PB=PD,
都是等边三角形知PA=PB=PD,
所以OA=OB=OD,即点O为正方形ABED对角线的交点,
故 ,从而
,从而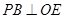 .
.
因为O是BD的中点,E是BC的中点,
所以OE//CD.因此 .
.

(Ⅱ)解:取PD的中点F,连结OF,则OF//PB.
由(Ⅰ)知, ,故
,故 .
.
又 ,
, ,
,
故 为等腰三角形,因此
为等腰三角形,因此 .
.
又 ,所以
,所以 平面PCD.
平面PCD.
因为AE//CD, 平面PCD,
平面PCD, 平面PCD,所以AE//平面PCD.
平面PCD,所以AE//平面PCD.
因此O到平面PCD的距离OF就是A到平面PCD的距离,而 ,
,
所以A至平面PCD的距离为1.
(1)解题的关键是辅助线的添加,取BC的中点E是入手点,然后借助三垂线定理进行证明;(2)求点面距的求解方法比较多,在解题过程中,如何根据题设条件恰当选择相适应的方法是比较棘手的问题。根据解题经验,总结下面常用的技巧:(1)若直接能够确定点在平面的射影,可考虑用直接法,找出点面距.一般在一些规则的几何体中,顶点在底面的射影比较容易确定.如有时要利用两个平面垂直的性质,在其中一个平面内作两个平面交线的垂线即得;(2)如果能够构造出三棱锥,要找的点面距恰好是三棱锥的高,此时利用等体积法比较简单,但是应该明确另一个顶点到对应底面的距离和底面面积两个量,才能顺利求解,计算过程较为麻烦,但是不用添加辅助线找垂线段. (3)若不易找出射影位置,可考虑利用转移的方法,即把不易求的点到平面的距离借助转移手法,变为求另外一点到平面的距离,然后通过这两点到平面的距离的数量关系求得所求距离的方法,常用的手段有平行转移和等比例转移.
【考点定位】本题考查线线垂直的证明和二面角的求解,考查学生的空间想象能力和计算能力。


科目:高中数学 来源:2010年吉林省东北师大附中高一下学期期中考试数学 题型:解答题
(本题满分10分)
如图,四棱锥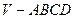 中,底面
中,底面 是边长为2的正方形,其余四个侧面都是侧棱长为
是边长为2的正方形,其余四个侧面都是侧棱长为 的等腰三角形,且
的等腰三角形,且 .
.
(1)求证: 平面
平面 ;
;
(2)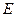 是
是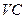 的中点,求
的中点,求 与平面
与平面 所成角的正切值.
所成角的正切值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年湖南长沙重点中学高三上学期第三次月考文科数学试卷(解析版) 题型:选择题
如图,某三棱锥的三视图都是直角边为 的等腰直角三角形,则该三棱锥的四个面的面积中最大的是( )
的等腰直角三角形,则该三棱锥的四个面的面积中最大的是( )

A.1
B. C.2
D.
C.2
D.
查看答案和解析>>
科目:高中数学 来源:2010年黑龙江省高二上学期期中考试数学理卷 题型:解答题
如图,四棱锥 中,底面
中,底面 是矩形,
是矩形,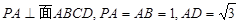 ,点
,点 是
是 的中点,点
的中点,点 在边
在边 上移动。
上移动。
1)点 为
为 的中点时,试判断
的中点时,试判断 与平面
与平面 的位置关系,并说明理由。
的位置关系,并说明理由。
2)证明:无论点 在边
在边 的何处,都有
的何处,都有
3)当 等于何值时,
等于何值时, 与平面
与平面 所成角的大小为
所成角的大小为 .(12分)
.(12分)

查看答案和解析>>
科目:高中数学 来源:2010年山西省高一上学期期中考试数学试卷 题型:解答题
如图,四棱锥 中,底面
中,底面 是矩形,
是矩形, ,点
,点 是
是 的中点,点
的中点,点 在边
在边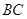 上移动。
上移动。
1)点 为
为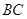 的中点时,试判断
的中点时,试判断 与平面
与平面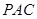 的位置关系,并说明理由。
的位置关系,并说明理由。
2)证明:无论点 在边
在边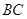 的何处,都有
的何处,都有
3)当 等于何值时,
等于何值时, 与平面
与平面 所成角的大小为
所成角的大小为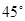 .(12分)
.(12分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com