
【题目】已知幂函数f(x)=x![]() (m∈N*).
(m∈N*).
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若该函数还经过点(2, ![]() ),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
),试确定m的值,并求满足条件f(2-a)>f(a-1)的实数a的取值范围.
【答案】(1)详见解析;(2)详见解析.
【解析】试题分析:(1)先判断幂函数的指数的奇偶,由m与m+1中必定有一个为偶数,可知m2+m为偶数,可得函数开偶次方,即函数定义域为[0,+∞),且在定义域内单调递增;(2)由过点(2, ![]() )和m∈N*求出m的值,进而得出函数的定义域和单调性,列出不等式解出a的范围即可.
)和m∈N*求出m的值,进而得出函数的定义域和单调性,列出不等式解出a的范围即可.
试题解析:
(1)∵m2+m=m(m+1),m∈N*,
∴m与m+1中必定有一个为偶数,
∴m2+m为偶数,
∴函数f(x)=x![]() (m∈N*)的定义域为[0,+∞),并且该函数在其定义域上为增函数.
(m∈N*)的定义域为[0,+∞),并且该函数在其定义域上为增函数.
(2)∵函数f(x)经过点(2,![]() ),
),
∴![]() =2
=2![]() ,即2
,即2![]() =2
=2![]() ,
,
∴m2+m=2,即m2+m-2=0.
∴m=1或m=-2.
又∵m∈N*,∴m=1.
∵f(x)在[0,+∞)上是增函数,
∴由f(2-a)>f(a-1)得
 解得1≤a<
解得1≤a<![]() .
.
故m的值为1,满足条件f(2-a)>f(a-1)的实数a的取值范围为![]() .
.
点睛:本题考查幂函数的定义和性质,属于中档题. 第一问先判断幂函数的指数的奇偶,由m与m+1中必定有一个为偶数,可知m2+m为偶数,可得函数开偶次方,即函数定义域为[0,+∞),且在定义域内单调递增;第二问由过点(2, ![]() )和m∈N*求出m的值,进而得出函数的定义域和单调性, 写出f(2-a)>f(a-1)的等价条件求解即可.
)和m∈N*求出m的值,进而得出函数的定义域和单调性, 写出f(2-a)>f(a-1)的等价条件求解即可.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)在R上是单调递减的一次函数,且f(f(x))=4x-1.
(1)求f(x);
(2)求函数y=f(x)+x2-x在x∈[-1,2]上的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1: ![]() (t为参数)曲线C2:
(t为参数)曲线C2:![]() +y2=4.
+y2=4.
(1)在同一平面直角坐标系中,将曲线C2上的点按坐标变换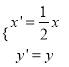 后得到曲线C′。求曲线C′的普通方程,并写出它的参数方程;
后得到曲线C′。求曲线C′的普通方程,并写出它的参数方程;
(2)若C1上的点P对应的参数为t=π/2,Q为C′上的动点,求PQ中点M到直线C3: ![]() (t为参数)的距离的最小值
(t为参数)的距离的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() .若直线
.若直线![]() 与圆C相交于不同的两点P,Q.
与圆C相交于不同的两点P,Q.
(Ⅰ)写出圆C的直角坐标方程,并求圆心的坐标与半径;
(Ⅱ)若弦长|PQ|=4,求直线![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了制定合理的节电方案,供电局对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照![]() ,
,![]() 分成9组,制成了如图所示的频率直方图.
分成9组,制成了如图所示的频率直方图.
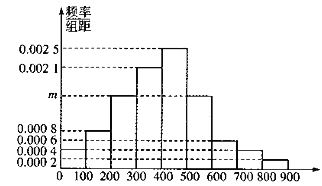
(1)求直方图中![]() 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;
(2)从样本里月均用电量不低于700度的用户中随机抽取4户,用![]() 表示月均用电量不低于800度的用户数,求随机变量
表示月均用电量不低于800度的用户数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(10分)设![]() 和
和![]() 分别是先后抛掷一枚骰子得到的点数,用随机变量
分别是先后抛掷一枚骰子得到的点数,用随机变量![]() 表示方程
表示方程
![]() 实根的个数(重根按一个计).
实根的个数(重根按一个计).
(Ⅰ)求方程![]() 有实根的概率;
有实根的概率;
(Ⅱ)求![]() 的分布列和数学期望;
的分布列和数学期望;
(Ⅲ)求在先后两次出现的点数中有5的条件下,方程![]() 有实根的概率.
有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两个正数a,b,可按规则![]() 扩充为一个新数c,在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
扩充为一个新数c,在a,b,c三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
(1)若a=1,b=3,按上述规则操作三次,扩充所得的数是_____________;
(2)若p>q>0,经过6次操作后扩充所得的数为![]() (m,n为正整数),
(m,n为正整数),
则m,n的值分别为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com