
| A. | 2 | B. | 6 | C. | $\frac{5}{2}$ | D. | $\frac{10}{3}$ |
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | (0,$\frac{1}{2}$] | C. | ($\frac{1}{2}$,1) | D. | [$\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-5,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1) | B. | (-5,1) | ||
| C. | (-5,-1) | D. | (-5,-1)∪(-1,-$\frac{1}{2}$)∪(-$\frac{1}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 27 | B. | 3 | C. | 27或3 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年内蒙古高二文上月考一数学试卷(解析版) 题型:选择题
已知双曲线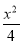 -
-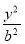 =1的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )
=1的右焦点与抛物线y2=12x的焦点重合,则该双曲线的焦点到其渐近线的距离等于( )
A.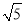 B.4
B.4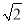 C.3 D.5
C.3 D.5
查看答案和解析>>
科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(文)试卷(解析版) 题型:选择题
如图,用一边长为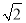 的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将表面积为
的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将表面积为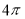 的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为( )
的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为( )
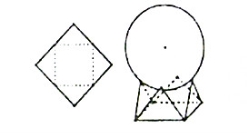
A.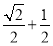 B.
B.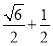 C.
C. 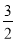 D.
D.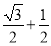
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com