
【题目】已知:椭圆![]() 的离心率为
的离心率为![]() ,且
,且![]() ,过左焦点
,过左焦点![]() 作一条直线交椭圆于
作一条直线交椭圆于![]() 、
、![]() 两点,过线段
两点,过线段![]() 的中点
的中点![]() 作
作![]() 的垂线交
的垂线交![]() 轴于点
轴于点![]() .
.
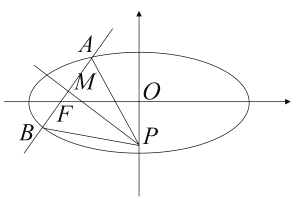
(1)求椭圆方程;
(2)当![]() 面积最大时,求直线
面积最大时,求直线![]() 的斜率.
的斜率.
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源: 题型:
【题目】造纸术是我国古代四大发明之一,纸张的规格是指纸张制成后,经过修整切边,裁成一定的尺寸.现在我国采用国际标准,规定以![]() 、
、![]() 、…、
、…、![]() ;
;![]() 、
、![]() 、…、
、…、![]() 等标记来表示纸张的幅面规格.复印纸幅面规格只采用
等标记来表示纸张的幅面规格.复印纸幅面规格只采用![]() 系列和
系列和![]() 系列,共中
系列,共中![]() 系列的幅面规格为:①
系列的幅面规格为:①![]() 规格的纸张的幅宽(以
规格的纸张的幅宽(以![]() 表示)和长度(以
表示)和长度(以![]() 表示)的比例关系为
表示)的比例关系为![]() ;②将
;②将![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,
规格,![]() 纸张沿长度方向对开成两等分,便成为
纸张沿长度方向对开成两等分,便成为![]() 规格,…,如此对开至
规格,…,如此对开至![]() 规格.现有
规格.现有![]() 、
、![]() 、
、![]() 、…、
、…、![]() 纸各一张.若
纸各一张.若![]() 纸的面积为
纸的面积为![]() .则这9张纸的面积之和等于__________
.则这9张纸的面积之和等于__________![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】成书于公元一世纪的我国经典数学著作《九章算术》中有这样一道名题,就是“引葭赴岸”问题,题目是:“今有池方一丈,点生其中央,出水一尺,引葭赶岸,适马岸齐,问水深,葭长各几何?”题意是:有一正方形池塘,边长为一丈(10尺),有棵芦苇长在它的正中央,高出水面部分有1尺长,把芦苇拉向岸边,恰好碰到沿岸(池塘一边的中点),则水深为__________尺,芦苇长__________尺.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn,a1![]() ,公比q>0,S1+a1,S3+a3,S2+a2成等差数列.
,公比q>0,S1+a1,S3+a3,S2+a2成等差数列.
(1)求{an};
(2)设bn![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着国家综合国力的提升和科技的进步,截至![]() 年底,中国铁路运营里程达
年底,中国铁路运营里程达![]() 万千米,这个数字比
万千米,这个数字比![]() 年增长了
年增长了![]() 倍;高铁运营里程突破
倍;高铁运营里程突破![]() 万千米,占世界高铁运营里程的
万千米,占世界高铁运营里程的![]() 以上,居世界第一位.如表截取了
以上,居世界第一位.如表截取了![]() 年中国高铁密度的发展情况(单位:千米/万平方千米).
年中国高铁密度的发展情况(单位:千米/万平方千米).
年份 |
|
|
|
|
|
年份代码 |
|
|
|
|
|
高铁密度 |
|
|
|
|
|
已知高铁密度![]() 与年份代码
与年份代码![]() 之间满足关系式
之间满足关系式![]() (
(![]() 为大于
为大于![]() 的常数).
的常数).
(1)根据所给数据,求![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() 位);
位);
(2)利用(1)的结论,预测到哪一年,高铁密度会超过![]() 千米/万平方千米.
千米/万平方千米.
参考公式:设具有线性相关系的两个变量![]() 的一组数据为
的一组数据为![]() ,则回归方程
,则回归方程![]() 的系数:
的系数: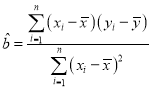 ,
,![]()
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() ,
,![]() 是某景区的两条道路(宽度忽略不计,
是某景区的两条道路(宽度忽略不计,![]() 为东西方向),Q为景区内一景点,A为道路
为东西方向),Q为景区内一景点,A为道路![]() 上一游客休息区,已知
上一游客休息区,已知![]() ,
,![]() (百米),Q到直线
(百米),Q到直线![]() ,
,![]() 的距离分别为3(百米),
的距离分别为3(百米),![]() (百米),现新修一条自A经过Q的有轨观光直路并延伸至道路
(百米),现新修一条自A经过Q的有轨观光直路并延伸至道路![]() 于点B,并在B处修建一游客休息区.
于点B,并在B处修建一游客休息区.
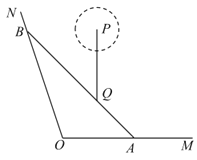
(1)求有轨观光直路![]() 的长;
的长;
(2)已知在景点Q的正北方6百米的P处有一大型组合音乐喷泉,喷泉表演一次的时长为9分钟,表演时,喷泉喷洒区域以P为圆心,r为半径变化,且t分钟时,![]() (百米)(
(百米)(![]() ,
,![]() ).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道
).当喷泉表演开始时,一观光车S(大小忽略不计)正从休息区B沿(1)中的轨道![]() 以
以![]() (百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
(百米/分钟)的速度开往休息区A,问:观光车在行驶途中是否会被喷泉喷洒到,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
18 | |||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: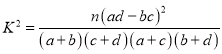 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com