
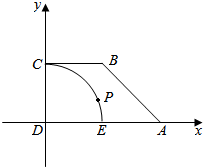
 已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.
已知直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=2,BC=DC=1,以D为圆心,DC为半径,作弧和AD交于点E,点P为劣弧CE上的动点,如图所示.分析 (1)建立坐标系,代入各点坐标计算;
(2)设P(cosα,sinα),用α表示出$\overrightarrow{PA}•\overrightarrow{PB}$,转化成三角函数求最值.
解答 解:(1)以DA所在直线为x轴,D为原点建立平面直角坐标系,
则 A(2,0),B(1,1),C(0,1),D(0,0),
$\overrightarrow{DA}$=(2,0),$\overrightarrow{DC}$=(0,1),∴$\overrightarrow{DA}+\overrightarrow{DC}$=(2,1).
∴|$\overrightarrow{DA}+DC$|=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$.
(2)设点$P(cosα,sinα),0≤α≤\frac{π}{2}$,
∴$\overrightarrow{PA}=(2-cosα,-sinα)$,$\overrightarrow{PB}=(1-cosα,1-sinα)$
∴$\overrightarrow{PA}•\overrightarrow{PB}=(2-cosα)(1-cosα)+(-sinα)(1-sinα)$=-(sinα+3cosα)+3=$-\sqrt{10}sin(α+φ)+3$,(sinφ=$\frac{\sqrt{10}}{10}$,cosφ=$\frac{3\sqrt{10}}{10}$)
∵$α∈[0,\frac{π}{2}],tanφ=3$
∴当sin(α+φ)=1时,$\overrightarrow{PA}•\overrightarrow{PB}$的取得最小值是$3-\sqrt{10}$.
点评 本题考查了平面向量在几何中的应用,建立坐标系是关键.


 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:解答题
 如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2或3 | B. | -1或6 | C. | 6 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 26 | 38 | 22 | 8 |

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{π}{3}$,$\frac{π}{6}$)? | B. | (-$\frac{π}{2}$,$\frac{π}{2}$)? | C. | (-$\frac{π}{3}$,$\frac{π}{3}$)?? | D. | (-$\frac{π}{6}$,$\frac{2π}{3}$)? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 24 | B. | -24 | C. | 12 | D. | -12 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “f(0)=0”是“函数f(x)是奇函数”的充要条件 | |
| B. | 若p:?x0∈R,x02-x0-1>0,则¬p:?x∈R,x2-x-1<0 | |
| C. | 若p∧q为假命题,则p,q均为假命题 | |
| D. | “若$α=\frac{π}{6}$,则$sinα=\frac{1}{2}$”的逆否命题为真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com