
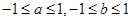 ,则函数f(x)=
,则函数f(x)= 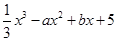 的两个极值点都在(0,1)内的概率为______
的两个极值点都在(0,1)内的概率为______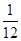
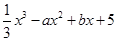 有极值对应的可行域面积的大小和实数a,b满足
有极值对应的可行域面积的大小和实数a,b满足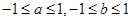 对应的图形面积的大小。
对应的图形面积的大小。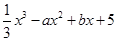 ∴f′(x)=x2-2ax+b,
∴f′(x)=x2-2ax+b,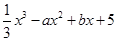 的两个极值点都在(0,1)内,
的两个极值点都在(0,1)内,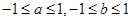 ,
,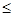 a
a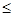 1,-1
1,-1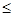 b
b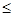 1的面积(图中正方形所示)为4,
1的面积(图中正方形所示)为4,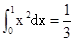 ,所求的概率为
,所求的概率为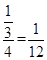


 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com