
【题目】设函数![]() ,
,![]() .
.
(1)讨论![]() 在
在![]() 上的单调性;
上的单调性;
(2)当![]() 时,若存在正实数
时,若存在正实数![]() ,使得对
,使得对![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]()
【解析】
(1)对![]() 求导,
求导,![]() 得到增区间,
得到增区间,![]() 得到减区间,注意对
得到减区间,注意对![]() 讨论. (2)要使得对
讨论. (2)要使得对![]() ,都有
,都有![]() ,只需研究
,只需研究![]() ,
,![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,去掉绝对值号有
,去掉绝对值号有![]() ,令
,令![]() ,对
,对![]() 求导 ,分
求导 ,分![]() 和
和![]() 两种情况研究单调性和最小值,注意
两种情况研究单调性和最小值,注意![]() 这一特殊函数值.
这一特殊函数值.
解:(1)由![]() ,得
,得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
当![]() 时,
时,
由![]() ,得
,得![]() ,即函数
,即函数![]() 在
在![]() 上单调递增,
上单调递增,
由![]() ,得
,得![]() ,即函数
,即函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() ,
,![]() 在
在![]() 上恒成立,即函数
上恒成立,即函数![]() 在
在![]() 上单调递增.
上单调递增.
综合以上有,
![]() ,即函数
,即函数![]() 在
在![]() 上单调递增.
上单调递增.
![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)由(1)知,
当![]() 时,
时,![]() 在
在![]() 上单调递减,且
上单调递减,且![]()
![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() ,此时,
,此时,![]()
则由![]() ,得
,得![]() .
.
设![]() ,
,
令![]() 得
得![]() ,令
,令![]() 得
得![]() .
.
若![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() 在
在![]() 上单调递减,注意到
上单调递减,注意到![]() ,
,
∴对任意![]() ,
,![]() ,与题设不符;
,与题设不符;
若![]() ,则
,则![]() ,
,![]() ,
,
∴![]() 在
在![]() 上单调递增,
上单调递增,
∵![]() ,∴对任意
,∴对任意![]() ,
,![]() 符合题意.
符合题意.
此时取![]() ,
,
可得对任意![]() ,都有
,都有![]() .
.
综上所述,![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,以
,以![]() 为圆心过椭圆左顶点
为圆心过椭圆左顶点![]() 的圆与直线
的圆与直线![]() 相切于
相切于![]() ,且满足
,且满足![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 右焦点
右焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,问
,问![]() 内切圆面积是否有最大值?若有,求出最大值;若没有,说明理由.
内切圆面积是否有最大值?若有,求出最大值;若没有,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点![]() 为正方形
为正方形![]() 边
边![]() 上异于点
上异于点![]() ,
,![]() 的动点,将
的动点,将![]() 沿
沿![]() 翻折成
翻折成![]() ,在翻折过程中,下列说法正确的是( )
,在翻折过程中,下列说法正确的是( )
A.存在点![]() 和某一翻折位置,使得
和某一翻折位置,使得![]()
B.存在点![]() 和某一翻折位置,使得
和某一翻折位置,使得![]() 平面
平面![]()
C.存在点![]() 和某一翻折位置,使得直线
和某一翻折位置,使得直线![]() 与平面
与平面![]() 所成的角为45°
所成的角为45°
D.存在点![]() 和某一翻折位置,使得二面角
和某一翻折位置,使得二面角![]() 的大小为60°
的大小为60°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知![]() 为椭圆
为椭圆![]() 的上顶点,P为椭圆E上异于上、下顶点的一个动点.当点P的横坐标为
的上顶点,P为椭圆E上异于上、下顶点的一个动点.当点P的横坐标为![]() 时,
时,![]() .
.
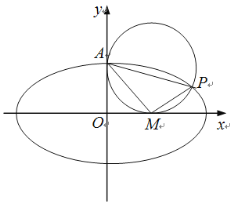
(1)求椭圆E的标准方程;
(2)设M为x轴的正半轴上的一个动点.
①若点P在第一象限内,且以AP为直径的圆恰好与x轴相切于点M,求AP的长.
②若![]() ,是否存在点N,满足
,是否存在点N,满足![]() ,且AN的中点恰好在椭圆E上?若存在,求点N的坐标;若不存在,请说明理由.
,且AN的中点恰好在椭圆E上?若存在,求点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国法定劳动年龄是![]() 周岁至退休年龄(退休年龄一般指男
周岁至退休年龄(退休年龄一般指男![]() 周岁,女干部身份
周岁,女干部身份![]() 周岁,女工人
周岁,女工人![]() 周岁).为更好了解我国劳动年龄人口变化情况,有关专家统计了
周岁).为更好了解我国劳动年龄人口变化情况,有关专家统计了![]() 年我国劳动年龄人口和
年我国劳动年龄人口和![]() 周岁人口数量(含预测),得到下表:
周岁人口数量(含预测),得到下表:
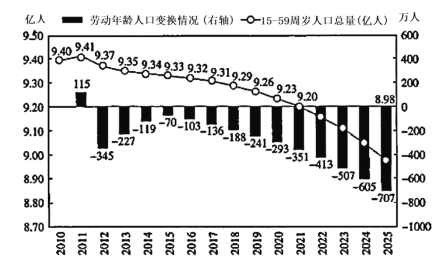
其中![]() 年劳动年龄人口是
年劳动年龄人口是![]() 亿人,则下列结论不正确的是( )
亿人,则下列结论不正确的是( )
A.![]() 年劳动年龄人口比
年劳动年龄人口比![]() 年减少了
年减少了![]() 万人以上
万人以上
B.![]() 这
这![]() 年
年![]() 周岁人口数的平均数是
周岁人口数的平均数是![]() 亿
亿
C.![]() 年,
年,![]() 周岁人口数每年的减少率都小于同年劳动人口每年的减少率
周岁人口数每年的减少率都小于同年劳动人口每年的减少率
D.![]() 年这
年这![]() 年
年![]() 周岁人口数的方差小于这
周岁人口数的方差小于这![]() 年劳动人口数的方差
年劳动人口数的方差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秉承“绿水青山就是金山银山”的发展理念,某市环保部门通过制定评分标准,先对本市的企业进行评估,评出四个等级,并根据等级给予相应的奖惩,如下表所示:
评估得分 |
|
|
|
|
评定等级 | 不合格 | 合格 | 良好 | 优秀 |
奖励(万元) |
|
|
|
|
环保部门对企业评估完成后,随机抽取了![]() 家企业的评估得分(
家企业的评估得分(![]() 分)为样本,得到如下频率分布表:
分)为样本,得到如下频率分布表:
评估得分 |
|
|
|
|
|
|
频率 |
|
|
|
|
|
|
其中![]() 、
、![]() 表示模糊不清的两个数字,但知道样本评估得分的平均数是
表示模糊不清的两个数字,但知道样本评估得分的平均数是![]() .
.
(1)现从样本外的数百个企业评估得分中随机抽取![]() 个,若以样本中频率为概率,求该家企业的奖励不少于
个,若以样本中频率为概率,求该家企业的奖励不少于![]() 万元的概率;
万元的概率;
(2)现从样本“不合格”、“合格”、“良好”三个等级中,按分层抽样的方法抽取![]() 家企业,再从这
家企业,再从这![]() 家企业随机抽取
家企业随机抽取![]() 家,求这两家企业所获奖励之和不少于
家,求这两家企业所获奖励之和不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() x∈R,其中a,b∈R.
x∈R,其中a,b∈R.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)若f(x)存在极值点x0,且f(x1)= f(x0),其中x1≠x0,求证:x1+2x0=3;
(Ⅲ)设a>0,函数g(x)= |f(x)|,求证:g(x)在区间[0,2]上的最大值不小于![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2|x+1|+|x-2|.
(1)求f(x)的最小值m;
(2)若a,b,c均为正实数,且满足a+b+c=m,求证:![]() +
+![]() +
+![]() ≥3.
≥3.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现在进入“互联网+”时代,大学生小张自己开了一家玩具店,他通过“互联网+”销售某种玩具,经过一段时间对一种玩具的销售情况进行统计,得5数据如下:
假定玩具的销售量![]() (百个)与玩具的销售价价格
(百个)与玩具的销售价价格![]() (元)之间存在相关关系:
(元)之间存在相关关系:
销售量 | 2 | 3 | 4 | 5 | 6 | 8 |
单个玩具的销售价 | 5.5 | 4.3 | 3.9 | 3.8 | 3.7 | 3.6 |
根据以上数据,小张分别借助甲、乙两种不同的回归模型,得到两个回归方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)以![]() 为解释变量,
为解释变量,![]() 为预报变量,作出散点图;
为预报变量,作出散点图;
(2)分别计算模型甲与模型乙的残差平方和![]() 及
及![]() ,并通过比较
,并通过比较![]() ,
,![]() 大小,判断哪个模型拟后效果更好.
大小,判断哪个模型拟后效果更好.
(3)若—个玩具进价0.5元,依据(2)中拟合效果好的模型判断该玩具店有无亏损的可能?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com