
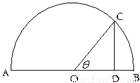
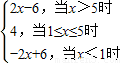 Ј¬їЙЦЄgЈЁxЈ©min=4Ј¬ЎаaЈј4Ј®
Ј¬їЙЦЄgЈЁxЈ©min=4Ј¬ЎаaЈј4Ј® Ј®
Ј® =3DBЈ¬ЎаOD=r-DB=2DBЈ®
=3DBЈ¬ЎаOD=r-DB=2DBЈ® =
= =
= Ј®
Ј® Ј¬јґy=x+2Ј®
Ј¬јґy=x+2Ј® Ј¬y=x+2Ј®
Ј¬y=x+2Ј®

 Мб·Ц°Щ·Ц°ЩјмІвѕнПµБРґр°ё
Мб·Ц°Щ·Ц°ЩјмІвѕнПµБРґр°ё ±¦±ґјЖ»®ЖЪД©іеґМ¶б100·ЦПµБРґр°ё
±¦±ґјЖ»®ЖЪД©іеґМ¶б100·ЦПµБРґр°ё ДЬїјКФИ«ДЬ100·ЦПµБРґр°ё
ДЬїјКФИ«ДЬ100·ЦПµБРґр°ё
| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
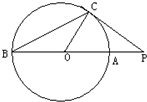 СЎЧцМвЈЁЗлїјЙъФЪТФПВИэёцРЎМвЦРИОСЎТ»МвЧчґрЈ¬Из№ы¶аЧцЈ¬Фт°ґЛщЧцµДµЪТ»МвЖАФДјЗ·ЦЈ©
СЎЧцМвЈЁЗлїјЙъФЪТФПВИэёцРЎМвЦРИОСЎТ»МвЧчґрЈ¬Из№ы¶аЧцЈ¬Фт°ґЛщЧцµДµЪТ»МвЖАФДјЗ·ЦЈ©
|
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
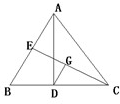 СЎЧцМвЈЁЗлїјЙъФЪТФПВИэёцРЎМвЦРИОСЎТ»МвЧчґрЈ¬Из№ы¶аЧцЈ¬Фт°ґЛщЧцµДµЪТ»МвЖАФДјЗ·ЦЈ©
СЎЧцМвЈЁЗлїјЙъФЪТФПВИэёцРЎМвЦРИОСЎТ»МвЧчґрЈ¬Из№ы¶аЧцЈ¬Фт°ґЛщЧцµДµЪТ»МвЖАФДјЗ·ЦЈ©
|
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
| ||
| 2 |
| ||
| 2 |

Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
 СЎЧцМвЈЁЗлїјЙъФЪТФПВИэёцРЎМвЦРИОСЎТ»МвЧчґрЈ¬Из№ы¶аЧцЈ¬Фт°ґЛщЧцµДµЪТ»МвЖАФДјЗ·ЦЈ©
СЎЧцМвЈЁЗлїјЙъФЪТФПВИэёцРЎМвЦРИОСЎТ»МвЧчґрЈ¬Из№ы¶аЧцЈ¬Фт°ґЛщЧцµДµЪТ»МвЖАФДјЗ·ЦЈ©| ¦Р |
| 4 |
| ||
| 2 |
| 2 |
| 2 |
| 1 |
| x |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєёЯЦРКэС§ АґФґЈє МвРНЈє
 ЈЁ2011•ОјДПИэДЈЈ©СЎЧцМвЈЁЗлїјЙъФЪТФПВИэёцРЎМвЦРИОСЎТ»МвЧчґрЈ¬Из№ы¶аЧцЈ¬Фт°ґЛщЧцµДµЪТ»МвЖАФДјЗ·ЦЈ©
ЈЁ2011•ОјДПИэДЈЈ©СЎЧцМвЈЁЗлїјЙъФЪТФПВИэёцРЎМвЦРИОСЎТ»МвЧчґрЈ¬Из№ы¶аЧцЈ¬Фт°ґЛщЧцµДµЪТ»МвЖАФДјЗ·ЦЈ©| 3 |
| 3 |
|
| ¦Р |
| 3 |
Ійїґґр°ёєНЅвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com