
| A. | -2016 | B. | -2015 | C. | -2014 | D. | -1007 |
分析 利用两角差的正切公式化简即得结论.
解答 解:记an=tan$\frac{n}{9}$π•tan$\frac{n+1}{9}$π,
则an=$\frac{tan\frac{n}{9}π-tan\frac{n+1}{9}π}{tan(\frac{n}{9}-\frac{n+1}{9})π}$-1=-1+$\frac{1}{tan\frac{π}{9}}$(tan$\frac{n+1}{9}$π-tan$\frac{n}{9}$π),
∴S2015=-2015+$\frac{1}{tan\frac{π}{9}}$(tan$\frac{2015+1}{9}$π-tan$\frac{2014+1}{9}$π+tan$\frac{2014+1}{9}$π-tan$\frac{2013+1}{9}$π+…+$tan\frac{2}{9}π$-tan$\frac{π}{9}$)
=-2015+$\frac{1}{tan\frac{π}{9}}$(tan$\frac{2015+1}{9}$π-tan$\frac{π}{9}$)
=-2015+$\frac{1}{tan\frac{π}{9}}$(tan224π-tan$\frac{π}{9}$)
=-2015+$\frac{1}{tan\frac{π}{9}}$(0-tan$\frac{π}{9}$)
=-2016,
故选:A.
点评 本题考查数列的求和,利用两角差的正切公式化简是解决本题的关键,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{27}$ | B. | $\frac{1}{27}$ | C. | $\frac{2}{9}$ | D. | $\frac{26}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,在一个不规则多边形内随机撒入200粒麦粒(麦粒落到任何位置可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为( )
如图,在一个不规则多边形内随机撒入200粒麦粒(麦粒落到任何位置可能性相等),恰有40粒落入半径为1的圆内,则该多边形的面积约为( )| A. | 4π | B. | 5π | C. | 6π | D. | 7π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
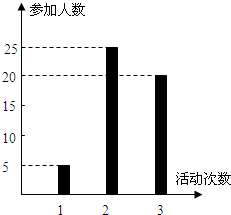 按照新课程的要求,高中学生在每学期都要至少参加一次社会实践活动(以下简称活动).该校高2010级一班50名学生在上学期参加活动的次数统计如图所示.
按照新课程的要求,高中学生在每学期都要至少参加一次社会实践活动(以下简称活动).该校高2010级一班50名学生在上学期参加活动的次数统计如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com