
【题目】如图所示,摩天轮的半径为![]() ,
,![]() 点距地面的高度为
点距地面的高度为![]() ,摩天轮按逆时针方向作匀速运动,且每
,摩天轮按逆时针方向作匀速运动,且每![]() 转一圈,摩天轮上点
转一圈,摩天轮上点![]() 的起始位置在最高点.
的起始位置在最高点.

(1)试确定点![]() 距离地面的高度
距离地面的高度![]() (单位:
(单位:![]() )关于旋转时间
)关于旋转时间![]() (单位:
(单位:![]() )的函数关系式;
)的函数关系式;
(2)在摩天轮转动一圈内,有多长时间![]() 点距离地面超过
点距离地面超过![]() ?
?
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由图形知,以点O为原点,![]() 所在直线为y轴,过O且与
所在直线为y轴,过O且与![]() 垂直的向右的方向为x轴建立坐标系,得出点P的纵坐标,由起始位置得
垂直的向右的方向为x轴建立坐标系,得出点P的纵坐标,由起始位置得![]() 即可得出在时刻tmin时P点距离地面的高度的函数;
即可得出在时刻tmin时P点距离地面的高度的函数;
(2)由(1)中的函数,令函数值大于70解不等式即可得出P点距离地面超过70m的时间.
(1)建立如图所示的平面直角坐标系,
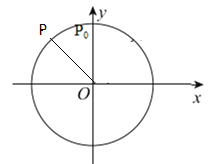
设![]() 是以
是以![]() 轴正半轴为始边,
轴正半轴为始边,![]() (
(![]() 表示点
表示点![]() 的起始位置)为终边的角,
的起始位置)为终边的角,
由题点![]() 的起始位置在最高点知,
的起始位置在最高点知,![]() ,
,
又由题知![]() 在
在![]() 内转过的角为
内转过的角为![]() ,即
,即![]() ,
,
所以以![]() 轴正半轴为始边,
轴正半轴为始边,![]() 为终边的角为
为终边的角为![]() ,
,
即![]() 点纵坐标为
点纵坐标为![]() ,
,
所以点![]() 距离地面的高度
距离地面的高度![]() 关于旋转时间
关于旋转时间![]() 的函数关系式是
的函数关系式是![]() ,
,
化简得![]() .
.
(2)当![]() 时,解得
时,解得![]() ,
,
又![]() ,所以符合题意的时间段为
,所以符合题意的时间段为![]() 或
或![]() ,即在摩天轮转动一圈内,有
,即在摩天轮转动一圈内,有![]()
![]() 点距离地面超过
点距离地面超过![]() .
.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
【题目】函数![]() 满足以下4个条件.
满足以下4个条件.
①函数![]() 的定义域是
的定义域是![]() ,且其图象是一条连续不断的曲线;
,且其图象是一条连续不断的曲线;
②函数![]() 在
在![]() 不是单调函数;
不是单调函数;
③函数![]() 是偶函数;
是偶函数;
④函数![]() 恰有2个零点.
恰有2个零点.
(1)写出函数![]() 的一个解析式;
的一个解析式;
(2)画出所写函数![]() 的解析式的简图;
的解析式的简图;
(3)证明![]() 满足结论③及④.
满足结论③及④.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机生产企业为了解消费者对某款手机的认同情况,通过销售部随机抽取50名购买该款手机的消费者,并发出问卷调查(满分50分),该问卷只有20份给予回复,这20份的评分如下:
男 | 47,36,28,48,48,44,50,46,50,37,35,49 |
女 | 38,37,50,36,38,45,29,39 |
(1)完成下面的茎叶图,并求12名男消费者评分的中位数与8名女消费者评分的众数及平均值;
男 | 女 | |
2 | ||
3 | ||
4 | ||
5 |
满意 | 不满意 | 合计 | |
男 | |||
女 | |||
合计 |
(2)若大于40分为“满意”,否则为“不满意”,完成上面的![]() 列联表,并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关;
列联表,并判断是否有95%的把握认为消费者对该款手机的“满意度”与性别有关;
(3)若从回复的20名消费者中按性别用分层抽样的方法抽取5人,再从这5人中随机抽取2人作进一步调查,求至少有1名女性消费者被抽到的概率.
附:
| 0.05 | 0.025 | 0.01 |
| 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司的新能源产品上市后在国内外同时销售,已知第一批产品上市销售40天内全部售完,该公司对这批产品上市后的国内外市场销售情况进行了跟踪调查,如图所示,其中图①中的折线表示的是国外市场的日销售量与上市时间的关系;图②中的抛物线表示的是国内市场的日销售量与上市时间的关系;下表表示的是产品广告费用、产品成本、产品销售价格与上市时间的关系.
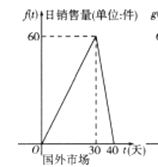 图① 图②
图① 图②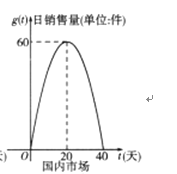
第t天产品广告费用(单位:万元) | 每件产品成本(单位:万元) | 每件产品销售价格(单位:万元) | |
|
| 3 | 6 |
| 10 | 3 | 5 |
(1)分别写出国外市场的日销售量![]() 、国内市场的日销售量
、国内市场的日销售量![]() 与产品上市时间t的函数关系式;
与产品上市时间t的函数关系式;
(2)产品上市后的哪几天,这家公司的日销售利润超过260万元?
(日销售利润=(单件产品销售价-单件产品成本)×日销售量-当天广告费用,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列![]() 中,已知
中,已知![]() ,对于任意的
,对于任意的![]() ,有
,有![]() .
.
(1)求数列![]() 的通项公式.
的通项公式.
(2)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
(3)设![]() ,是否存在实数
,是否存在实数![]() ,当
,当![]() 时,
时,![]() 恒成立?若存在,求实数
恒成立?若存在,求实数![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过市场调查,某种商品在销售中有如下关系:第x(![]() )天的销售价格(单位:元/件)为
)天的销售价格(单位:元/件)为![]() ,第x天的销售量(单位:件)为
,第x天的销售量(单位:件)为![]() (
(![]() 为常数),且在第20天该商品的销售收入为600元(销售收入=销售价格×销售量).
为常数),且在第20天该商品的销售收入为600元(销售收入=销售价格×销售量).
(1)求a的值,并求第15天该商品的销售收入;
(2)求在这30天中,该商品日销售收入y的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的定义域为
的定义域为![]() ,部分对应值如下表.
,部分对应值如下表.
x |
| 0 | 4 | 5 |
| 1 | 2 | 2 | 1 |
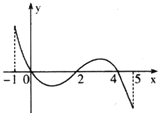
![]() 的导函数
的导函数![]() 的图象如图所示:下列关于
的图象如图所示:下列关于![]() 的命题:
的命题:
![]() 函数
函数![]() 是周期函数;
是周期函数;
![]() 函数
函数![]() 在
在![]() 是减函数;
是减函数;
![]() 如果当
如果当![]() 时,
时,![]() 的最大值是2,那么t的最大值为4;
的最大值是2,那么t的最大值为4;
![]() 函数
函数![]() 的零点个数可能为0、1、2、3、4个.
的零点个数可能为0、1、2、3、4个.
其中正确命题的序号是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】暑假期间,某旅行社为吸引游客去某风景区旅游,推出如下收费标准:若旅行团人数不超过30,则每位游客需交费用600元;若旅行团人数超过30,则游客每多1人,每人交费额减少10元,直到达到70人为止.
(1)写出旅行团每人需交费用![]() (单位:元)与旅行团人数
(单位:元)与旅行团人数![]() 之间的函数关系式;
之间的函数关系式;
(2)旅行团人数为多少时,旅行社可以从该旅行团获得最大收入?最大收入是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
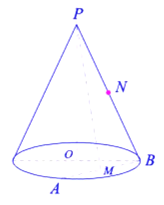
【题目】已知圆锥的顶点为![]() ,底面圆心为
,底面圆心为![]() ,母线长为
,母线长为![]() ,
,![]() ,
,![]() 、
、![]() 是底面半径,且:
是底面半径,且:![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为线段
为线段![]() 的中点,如图所示:
的中点,如图所示:
(1)求圆锥的表面积;
(2)求异面直线![]() 和
和![]() 所成的角的大小,并求
所成的角的大小,并求![]() 、
、![]() 两点在圆锥侧面上的最短距离.
两点在圆锥侧面上的最短距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com