
【题目】如图,在三棱柱![]() 中,侧面
中,侧面![]() 是为菱形,
是为菱形,![]() 在平面
在平面![]() 内的射影
内的射影![]() 恰为线段
恰为线段![]() 的中点.
的中点.
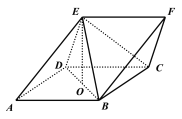
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,求二面角
,求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)连接![]() ,由线面垂直的判定方法可证得
,由线面垂直的判定方法可证得![]() 面
面![]() ,从而得到
,从而得到![]() ,根据平行关系可证得结论;
,根据平行关系可证得结论;
(2)以![]() 为坐标原点建立空间直角坐标系,利用二面角的空间向量求法可求得结果.
为坐标原点建立空间直角坐标系,利用二面角的空间向量求法可求得结果.
(1)证明:如图,连接![]() ,易知
,易知![]() .
.
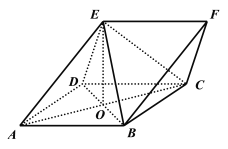
∵侧面![]() 是菱形,∴
是菱形,∴![]() .
.
由射影定义可知:![]() 面
面![]() ,又
,又![]() 面
面![]() ,∴
,∴![]() ,
,
而![]() ,且
,且![]() ,
,![]() 面
面![]() ,∴
,∴![]() 面
面![]() ,
,
![]() 平面
平面![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
(2)由(1)知:![]() ,
,![]() ,
,![]() ,,于是以
,,于是以![]() 为坐标原点,
为坐标原点,![]() ,
,![]() ,
,![]() 所在直线分别为
所在直线分别为![]() ,
,![]() ,
,![]() 轴建立空间直角坐标系,如图所示:
轴建立空间直角坐标系,如图所示:
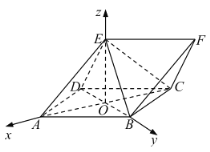
不妨设![]() .
.
∵在菱形![]() 中,
中,![]() ,∴
,∴![]() ,
,![]() .
.
在![]() 中,
中,![]() .
.
于是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
又由![]() ,可解得:
,可解得:![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则由![]() ,
,![]() 得
得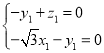 ,
,
令![]() ,则
,则![]() ,
,![]() ,即
,即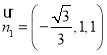 .
.
同理可得平面![]() 的法向量
的法向量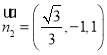 .
.
∴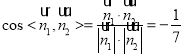 ,
,
![]() 二面角
二面角![]() 的平面角为锐角,
的平面角为锐角,![]() 所求的余弦值为
所求的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】车工刘师傅利用数控车床为某公司加工一种高科技易损零件,对之前加工的100个零件的加工时间进行统计,结果如下:
加工1个零件用时 | 20 | 25 | 30 | 35 |
频数(个) | 15 | 30 | 40 | 15 |
以加工这100个零件用时的频率代替概率.
(1)求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
(2)刘师傅准备给几个徒弟做一个加工该零件的讲座,用时40分钟,另外他打算在讲座前、讲座后各加工1个该零件作示范.求刘师傅讲座及加工2个零件作示范的总时间不超过100分钟的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入![]() ,
,![]() 的值分别为5,2,则输出
的值分别为5,2,则输出![]() 的值为( )
的值为( )
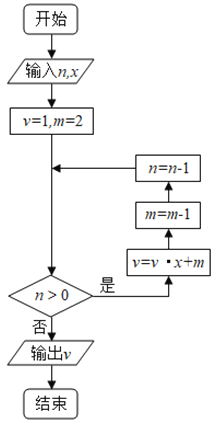
A.64B.68C.72D.133
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十二生肖是十二地支的形象化代表,即子(鼠)、丑(牛)、寅(虎)、卯(兔)、辰(龙)、巳(蛇)、午(马)、未(羊)、申(猴)、酉(鸡)、戌(狗)、亥(猪),每一个人的出生年份对应了十二种动物中的一种,即自己的属相.现有印着六种不同生肖图案(包含马、羊)的毛绒娃娃各一个,小张同学的属相为马,小李同学的属相为羊,现在这两位同学从这六个毛绒娃娃中各随机取一个(不放回),则这两位同学都拿到自己属相的毛绒娃娃的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若射线![]() 与曲线
与曲线![]() 相交于点
相交于点![]() ,将
,将![]() 逆时针旋转
逆时针旋转![]() 后,与曲线
后,与曲线![]() 相交于点
相交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,沿对角线
,沿对角线![]() 将
将![]() 折起,使点
折起,使点![]() 到达平面
到达平面![]() 外的点
外的点![]() 的位置,
的位置,
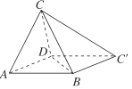
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当平面![]() 平面
平面![]() 时,求三棱锥
时,求三棱锥![]() 的外接球的体积;
的外接球的体积;
(3)当![]() 为等腰三角形时,求二面角
为等腰三角形时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥E-ABCD中,底面ABCD为正方形,![]() 平面CDE.已知
平面CDE.已知![]() ,
,![]() .
.
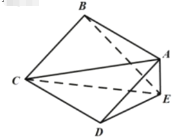
(1)证明:平面![]() 平面ABCD;
平面ABCD;
(2)求直线BE与平面ACE所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() 的右焦点为
的右焦点为![]() 点的坐标为
点的坐标为![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 是等腰直角三角形.
是等腰直角三角形.
(1)求椭圆![]() 的方程;
的方程;
(2)经过点![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,求
两点,求![]() 面积的最大值;
面积的最大值;
(3)是否存在直线![]() 交椭圆于
交椭圆于![]() 两点,使点
两点,使点![]() 为
为![]() 的垂心(垂心:三角形三边高线的交点)?若存在,求出直线
的垂心(垂心:三角形三边高线的交点)?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com