
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为
的半径为![]() ,圆心在
,圆心在![]() 上.
上.
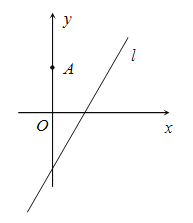
(Ⅰ)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线的方程;
的切线,求切线的方程;
(Ⅱ)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
【答案】(1)![]() 或者
或者![]() ;(2)
;(2)![]()
【解析】
试题分析:(1)由题意分析可知,圆心C既在直线![]() 上,又在直线
上,又在直线![]() 上,所以C为两条直线的交点,由
上,所以C为两条直线的交点,由![]() 解得C(3,2),所以圆C的方程为
解得C(3,2),所以圆C的方程为![]() ,过点A作圆C的切线,显然切线的斜率存在,设为k,则切线方程为
,过点A作圆C的切线,显然切线的斜率存在,设为k,则切线方程为![]() ,由于直线与圆C相切,所以圆心到直线的距离等于半径,即
,由于直线与圆C相切,所以圆心到直线的距离等于半径,即![]() ,即
,即![]() ,
,![]() ,解得
,解得![]() 或
或![]() ,所以所求切线方程为
,所以所求切线方程为![]() 或
或![]() ;(2)设圆心C(a,2a-4),则圆C的方程为
;(2)设圆心C(a,2a-4),则圆C的方程为![]() ,设圆C上点M(x,y),根据
,设圆C上点M(x,y),根据![]() ,有
,有![]() ,整理得到点M(x,y)的轨迹方程为
,整理得到点M(x,y)的轨迹方程为![]() ,设此方程为圆D,则点M既在圆C上,又在圆D上, 所以转化为圆C与圆D有交点,根据圆与圆的位置关系有:
,设此方程为圆D,则点M既在圆C上,又在圆D上, 所以转化为圆C与圆D有交点,根据圆与圆的位置关系有:![]() ,
,![]() ,即可求出
,即可求出![]() 的取值范围。
的取值范围。
试题解析:(1)由![]() 得圆心C为(3,2),∵圆
得圆心C为(3,2),∵圆![]() 的半径为
的半径为
∴圆![]() 的方程为:
的方程为: ![]()
显然切线的斜率一定存在,设所求圆C的切线方程为![]() ,即
,即![]()
∴![]() ∴
∴![]() ∴
∴![]() ∴
∴![]() 或者
或者![]()
∴所求圆C的切线方程为: ![]() 或者
或者![]()
即![]() 或者
或者![]()
(2)解:∵圆![]() 的圆心在在直线
的圆心在在直线![]() 上,所以,设圆心C为(a,2a-4)
上,所以,设圆心C为(a,2a-4)
则圆![]() 的方程为:
的方程为: ![]()
又∵![]() ∴设M为(x,y)则
∴设M为(x,y)则![]() 整理得:
整理得: ![]() 设为圆D
设为圆D
∴点M应该既在圆C上又在圆D上 即:圆C和圆D有交点
∴![]() 由
由![]() 得
得![]()
由![]() 得
得![]()
终上所述, ![]() 的取值范围为:
的取值范围为: ![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】梯形ABCD中,AB∥CD,AB平面α,CD平面α,则直线CD与平面α内的直线的位置关系只能是( )
A.平行
B.平行或异面
C.平行或相交
D.异面或相交
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
分组 |
|
|
|
|
|
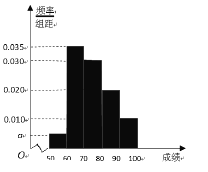
(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(3)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取2名,求其中恰有1人的分数不低于90分的概率?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人,女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动,男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动.
(1)根据以上数据建立一个![]() 的列联表;
的列联表;
(2)是否有97.5%的把握认为性别与休闲方式有关系?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】王昌龄《从军行》两句诗为“黄沙百战穿金甲,不破楼兰终不归”,其中后一句中“攻破楼兰”是“返回家乡”的( )
A. 充分条件 B. 必要条件 C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】算法的三种基本结构是( )
A. 顺序结构、模块结构、条件结构 B. 顺序结构、循环结构、模块结构
C. 顺序结构、条件结构、循环结构 D. 模块结构、条件结构、循环结构
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取
年下学期某市教育局对某校高三文科数学进行教学调研,从该校文科生中随机抽取![]() 名学生的数学成绩进行统计,将他们的成绩分成六段
名学生的数学成绩进行统计,将他们的成绩分成六段![]() 后得到如图所示的频率分布直方图.
后得到如图所示的频率分布直方图.

(1)求这40名学生中数学成绩不低于120分的学生人数;
(2)若从数学成绩![]() 内的学生中任意抽取2人,求成绩在
内的学生中任意抽取2人,求成绩在![]() 中至少有一人的概率.
中至少有一人的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了响应国家号召,某地决定分批建设保障性住房供给社会.首批计划用100万元购得一块土地,该土地可以建造每层1 000平方米的楼房,楼房的每平方米建筑费用与建筑高度有关,楼房每升高一层,整层楼每平方米建筑费用提高20元.已知建筑第5层楼房时,每平方米建筑费用为800元.
(1)若建筑第x层楼时,该楼房综合费用为y万元(综合费用是建筑费用与购地费用之和),写出y=f(x)的表达式;
(2)为了使该楼房每平方米的平均综合费用最低,应把楼层建成几层?此时平均综合费用为每平方米多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com