
【题目】试编写程序确定S=1+4+7+10+…中至少加到第几项时S≥300.
科目:高中数学 来源: 题型:
【题目】由直线与圆相切时,圆心与切点连线与直线垂直,想到平面与球相切时,球心与切点连线与平面垂直,用的是( )
A. 类比推理 B. 演绎推理 C. 归纳推理 D. 传递性推理
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】100件产品中有10件次品,从中任取7件,至少有5件次品的概率可以看成三个互斥事件的概率和,则这三个互斥事件分别是_____,_____和_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组对该校高三学生视力情况进行调查,在高三的全体1000名学生中随机抽取了若干名学生的体检表,并得到 如下直方图:

(Ⅰ)若直方图中前三组的频率成等比数列,后四组的频率成等差数列,试估计全年级视力在5.0以下的人数;
(Ⅱ)学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年纪名次在1~50名和951~1000名的学生进行了调查,得到如下数据:

根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(Ⅲ)在(Ⅱ)中调查的100名学生中,在不近视的学生中按照成绩是否在前50名分层抽样抽取了9人,
进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为![]() ,求
,求![]()
的分布列和数学期望.
附:

![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于不同的两点
于不同的两点![]() ,设线段
,设线段![]() 的中点为
的中点为![]() .
.
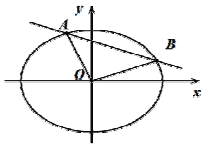
(1)求椭圆![]() 的方程;
的方程;
(2)当![]() 的面积为
的面积为![]() (其中
(其中![]() 为坐标原点)且
为坐标原点)且![]() 时,试问:在坐标平面上是否存在两个定点
时,试问:在坐标平面上是否存在两个定点![]() ,使得当直线
,使得当直线![]() 运动时,
运动时,![]() 为定值?若存在,求出点
为定值?若存在,求出点![]() 的坐标和定值;若不存在,请说明理由.
的坐标和定值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正项数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.
的等比数列.
(1)求证:数列![]() 是等差数列.
是等差数列.
(2)若![]() 的前
的前![]() 项和
项和![]() .
.
(3)在(2)条件下,是否存在常数![]() ,使得数列
,使得数列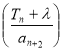 为等比数列?若存在,试求出
为等比数列?若存在,试求出![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面程序的功能为( )
S=1;
for i=1:1:10
S=(3^i)* S;
end
print(%io(2),S);
A. 用来计算3×103的值
B. 用来计算355的值
C. 用来计算310的值
D. 用来计算1×2×3×…×10的值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是一次函数,且f(-2)=-1,f(0)+f(2)=10,则f(x)的解析式为( )
A. 3x+5 B. 3x+2 C. 2x+3 D. 2x-3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com