
����Ŀ��![]() ��������
��������![]() ���ҹ��Ŵ�������ѧ����
���ҹ��Ŵ�������ѧ����![]() ���жԹ��ɶ�����������������һǧ���꣬����������һ�����⣺������Բ�����ڱ��У���֪��С
���жԹ��ɶ�����������������һǧ���꣬����������һ�����⣺������Բ�����ڱ��У���֪��С![]() �Ծ��֮����һ�磬�����һ��
�Ծ��֮����һ�磬�����һ��![]() �ʾ����Σ�������Ϊ������һԲ����ľ�ģ�����ǽ���У���֪���С���þ�ȥ��ò��ϣ������һ�磬�����һ��
�ʾ����Σ�������Ϊ������һԲ����ľ�ģ�����ǽ���У���֪���С���þ�ȥ��ò��ϣ������һ�磬�����һ��![]() �����Բ����ľ�ϵ�ֱ���Ƕ��٣���Ϊ1�ɵ�Բ����ľ�IJ�����Ƕ��ǽ���У�����ͼ��ͼ��ʾ
�����Բ����ľ�ϵ�ֱ���Ƕ��٣���Ϊ1�ɵ�Բ����ľ�IJ�����Ƕ��ǽ���У�����ͼ��ͼ��ʾ![]() ��Ӱ����Ϊ��Ƕ��ǽ���ڵIJ���
��Ӱ����Ϊ��Ƕ��ǽ���ڵIJ���![]() ��֪��
��֪��![]() �ߣ����θ�
�ߣ����θ�![]() �磬�����ľ����Ƕ��ǽ�е����ԼΪ( )(ע��1��
�磬�����ľ����Ƕ��ǽ�е����ԼΪ( )(ע��1��![]() ��
��![]() �磬
�磬![]() ��
��![]() )
)

A. 600������ B. 610������ C. 620������ D. 633������

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ξ���Ԥ��2013��1�·���ǰx���µ����������ĺ�p��x������λ�����ˣ���x�Ĺ�ϵ���Ƶ�����p��x��=![]() x��x+1����39��2x������x��N* �� ��x��12������֪��x�µ��˾����Ѷ�q��x������λ��Ԫ����x�Ľ��ƹ�ϵ��q��x��=
x��x+1����39��2x������x��N* �� ��x��12������֪��x�µ��˾����Ѷ�q��x������λ��Ԫ����x�Ľ��ƹ�ϵ��q��x��=
��I��д��2013���x�µ���������f��x������λ�����ˣ���x�ĺ�����ϵʽ��
��II������2013��ڼ������������ܶ������������������ܶ�Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ���IJ���ͼ����ͼ��ʾ��
���IJ���ͼ����ͼ��ʾ��
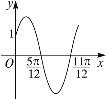
����������![]() �Ľ���ʽ��
�Ľ���ʽ��
����������![]() �ĵ����������䣮
�ĵ����������䣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ֳ������г���ij�ͺŵĶ���������ʹ������![]() �����ۼ۸�
�����ۼ۸�![]() ����λ����Ԫ/���������������õ����µĶ�Ӧ���ݣ�
����λ����Ԫ/���������������õ����µĶ�Ӧ���ݣ�
ʹ������ | 2 | 4 | 6 | 8 | 10 |
�ۼ� | 16 | 13 | 9.5 | 7 | 4.5 |
��1������![]() ����
����![]() �Ļع�ֱ�߷��̣����ο���ʽ��
�Ļع�ֱ�߷��̣����ο���ʽ��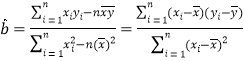 ,
, ![]() ����
����
��2����֪ÿ�����ͺ��������չ��۸�Ϊ![]() ��Ԫ�����ݣ�1��������Ļع鷽�̣�Ԥ��
��Ԫ�����ݣ�1��������Ļع鷽�̣�Ԥ��![]() Ϊ��ֵʱ������һ�����ͺ���������õ�����
Ϊ��ֵʱ������һ�����ͺ���������õ�����![]() ���
���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼��ij�������һ�������ߵ��������̣�����Աÿ��Ӹ��������������ȡ16���������������ߴ磨��λ�� ![]() �������ݳ����������飬������Ϊ��������������״̬������������ijߴ������̬�ֲ�
�������ݳ����������飬������Ϊ��������������״̬������������ijߴ������̬�ֲ�![]() ��
��
��1����������״̬��������![]() ��ʾһ���ڳ�ȡ��16���������ߴ���
��ʾһ���ڳ�ȡ��16���������ߴ���![]() ֮������������
֮������������![]() ��
��![]() ����ѧ������
����ѧ������
��2��һ���ڳ������У���������˳ߴ���![]() ֮������������Ϊ��������������һ����������̿��ܳ������쳣�������Ե�����������̽��м�飮
֮������������Ϊ��������������һ����������̿��ܳ������쳣�������Ե�����������̽��м�飮
��������˵����������������̷����ĺ����ԣ�
�����������Ǽ���Ա��һ���ڳ�ȡ��16������ijߴ磺
9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
�������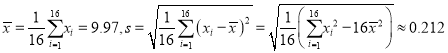 ������
������![]() Ϊ
Ϊ
��ȡ�ĵ�![]() ������ijߴ磬
������ijߴ磬 ![]() ��
��
������ƽ����![]() ��Ϊ
��Ϊ![]() �Ĺ���ֵ
�Ĺ���ֵ![]() ������������
������������![]() ��Ϊ
��Ϊ![]() �Ĺ���ֵ
�Ĺ���ֵ![]() �����ù���ֵ�ж��Ƿ���Ե�����������̽��м�飿��
�����ù���ֵ�ж��Ƿ���Ե�����������̽��м�飿��![]() ֮������ݣ���ʣ�µ����ݹ���
֮������ݣ���ʣ�µ����ݹ���![]() ��
��![]() ����ȷ��0.01����
����ȷ��0.01����
�������������![]() ������̬�ֲ�
������̬�ֲ�![]() ����
����![]() ��
�� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ϣ���˳���Сʯ����ɳ̲�ϰڳɸ�����״���о���.���磺
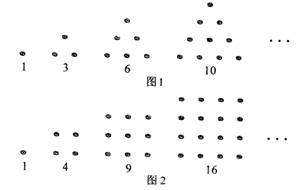
�����о���ͼ1�е�1��3��6��10������������Щ���ܹ���ʾ�������Σ������Ϊ�������������Ƶģ���ͼ2�е�1��4��9��16������������Ϊ��������.�������м��������������������������ǣ� ��
A. 36 B. 45 C. 99 D. 100
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����f��x��=x��aex��a��R����x��R����֪����y=f��x�����������x1 �� x2 �� ��x1��x2 ��
��1����a��ȡֵ��Χ��
��2��֤���� ![]() ����a�ļ�С������
����a�ļ�С������
��3��֤��x1+x2����a�ļ�С������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����л�װ��9����С��ͬ����Ų�ͬ��������5ֻ����4ֻ����Ϊ�˰Ѻ�����������ֿ�������ȡ��ֻ��ȡ��飬��ǡ�þ���5�γ�ȡ��飬���ð����а���ͺ������ֳ����ˣ��������ij�ȡ��ʽ����__________�֣����������� .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3��������4��Ů���������в�ͬҪ���£���ͬ�����з���������
��1��ȫ���ų�һ�У�����������������һ��;
��2��ȫ���ų�һ�У��С�Ů��������;
��3��ȫ���ų�һ�У����мײ�������ߣ��Ҳ������ұ�;
��4��ȫ���ų�һ�У����мס��ҡ������˴������ҵ�˳�䣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com