
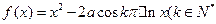 ,
,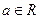 且
且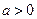 ).
).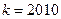 ,方程f (x) ="2" a x有惟一解时,求
,方程f (x) ="2" a x有惟一解时,求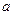 的值。
的值。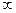 )上是增函数 ;当k是偶数时,f(x)在
)上是增函数 ;当k是偶数时,f(x)在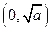 是减函数,在
是减函数,在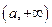 是增函数 (2)
是增函数 (2)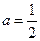
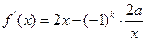 .
.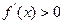 ,则f(x)在(0,+
,则f(x)在(0,+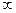 )上是增函数; ……(2分)
)上是增函数; ……(2分)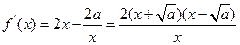 , ……(3分)
, ……(3分)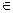
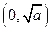 时,
时,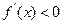 , 当x
, 当x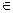
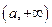 时,
时,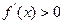 ,
, 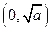 是减函数,在
是减函数,在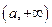 是增函数.……(5分)
是增函数.……(5分)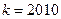 ,则
,则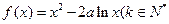 )
)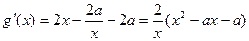 ,
,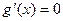 ,得
,得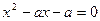 ,
,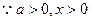
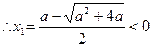 (舍去)
(舍去)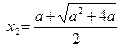 ……(7分)
……(7分)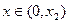 时,
时,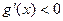 ,
,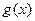 在
在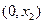 是单调递减函数;
是单调递减函数;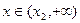 时,
时,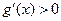 ,
,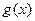 在
在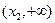 上是单调递增函数。
上是单调递增函数。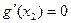 ,
,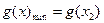 …………(8分)
…………(8分)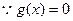 有唯一解,
有唯一解,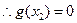
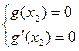 ,即
,即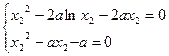 ………(9分)
………(9分)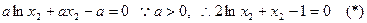 …………(10分)
…………(10分)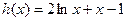 ,
,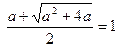 ,解得
,解得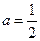 。…………(12分)
。…………(12分)

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源:不详 题型:解答题
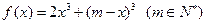 .
.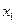 、
、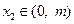 ,求证:①
,求证:①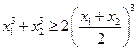 ;
;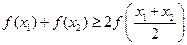 .
.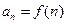 ,
,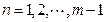 ,其中
,其中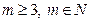 ,求证:
,求证: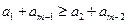 ;
;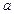 、
、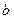 、
、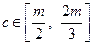 ,问:以
,问:以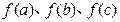 的值为长的三条线段是否可构成三角形?请说明理由.
的值为长的三条线段是否可构成三角形?请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
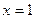 是函数
是函数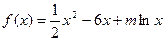 的一个极值点。
的一个极值点。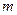 ;
;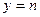 与函数
与函数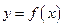 的图象有3个交点,求
的图象有3个交点,求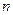 的取值范围;
的取值范围;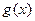 =(
=(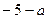 )
)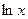 +
+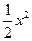 +(6-
+(6-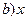 +2(
+2(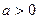 ),
),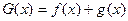 ,若
,若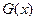 =0有两个零点
=0有两个零点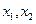 ,且
,且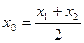 ,试探究
,试探究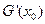 值的符号
值的符号
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
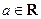 ,函数
,函数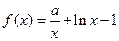 ,
,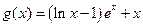 (其中
(其中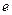 为自然对数的底数).
为自然对数的底数).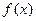 在区间
在区间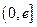 上的最小值;
上的最小值;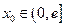 ,使曲线
,使曲线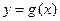 在点
在点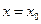 处的切线与
处的切线与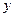 轴垂直? 若存在,求出
轴垂直? 若存在,求出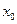 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com