练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数在一个周期内的简图如图所示，则函数的解析式为___________，方程的实根个数为__________.

    【答案】 63

    【解析】

    利用函数的最值可求A；利用函数图像过可求；利用函数的周期可求，从而可求出解析式， 在同一坐标系内作出函数和函数的图象，的最大值为2，令得，在内求出交点个数即可.

    解析显然，由图象过点，得，

    即，又，所以，

    又点在图象上，所以，即，

    由图象可知，是图象在y轴右侧部分与x轴的第二个交点，

    所以，解得，

    所以函数的解析式为.

    在同一坐标系内作出函数和函数的图象，

    如图.

    因为的最大值为2，令得.

    令，得，

    而，所以在内有31个形如的区间.

    而在每一个区间上，函数和函数的图象都有2个交点，

    故这两个图象在内有62个交点，另外在内还有1个交点.

    所以方程共有63个实根.

    故答案为：；63

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】海水受日月的引力，在一定的时候发生涨落的现象叫潮汐.一般地，早潮叫潮，晚潮叫汐.在通常情况下，船在涨潮时驶进航道，靠近码头；卸货后，在落潮时返回海洋.下面是某港口在某季节某天时间与水深（单位：米）的关系表：

    时刻

    0:00

    3:00

    6:00

    9:00

    12:00

    15:00

    18:00

    21:00

    24:00

    水深

    10.0

    13.0

    9.9

    7.0

    10.0

    13.0

    10.1

    7.0

    10.0

    （1）请用一个函数近似地描述这个港口的水深y与时间t的函数关系；

    （2）一般情况下，船舶航行时，船底离海底的距离为5米或5米以上认为是安全的（船舶停靠时，船底只要不碰海底即可）.某船吃水深度（船底离地面的距离）为6.5米.

    ①如果该船是旅游船，1:00进港，希望在同一天内安全出港，它至多能在港内停留多长时间（忽略进出港所需时间）？

    ②如果该船是货船，在2:00开始卸货，吃水深度以每小时0.5米的速度减少，由于台风等天气原因该船必须在10:00之前离开该港口，为了使卸下的货物尽可能多而且能安全驶离该港口，那么该船在什么整点时刻必须停止卸货（忽略出港所需时间）？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了推广一种新饮料，某饮料生产企业开展了有奖促销活动：将6罐这种饮料装一箱，每箱中都放置2罐能够中奖的饮料.若从一箱中随机抽出2罐，能中奖的概率为多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（12分）

    如图，四边形ABCD为梯形，AB//CD，平面ABCD，

    为BC的中点.

    （1）求证：平面平面PDE.

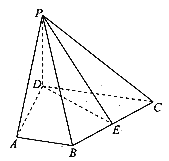    （2）在线段PC上是否存在一点F，使得PA//平面BDF？若存在，指出点F的位置，并证明；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】我校为了解学生喜欢通用技术课程“机器人制作”是否与学生性别有关，采用简单随机抽样的办法在我校高一年级抽出一个有60人的班级进行问卷调查，得到如下的列联表：

    喜欢

    不喜欢

    合计

    男生

    18

    女生

    6

    合计

    60

    已知从该班随机抽取1人为喜欢的概率是．

    (Ⅰ)请完成上面的列联表；

    (Ⅱ)根据列联表的数据，若按90%的可靠性要求，能否认为“喜欢与否和学生性别有关”？请说明理由．

    参考临界值表：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    参考公式：其中

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=sinxcosx+cos2x-．

    （Ⅰ）求函数f（x）的最小正周期及单调递增区间；

    （Ⅱ）将函数f（x）图象上各点的横坐标伸长到原来的2倍（纵坐标不变），得到函数g（x）的图象．若关于x的方程g（x）-k=0，在区间[0，]上有实数解，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某研究性学习小组为了调查研究学生玩手机对学习的影响，现抽取了30名学生，得到数据如表：

    玩手机

    不玩手机

    合计

    学习成绩优秀

    8

    学习成绩不优秀

    16

    合计

    30

    已知在全部的30人中随机抽取1人，抽到不玩手机的概率为.

    （1）请将2×2列联表补充完整；

    （2）能否在犯错误的概率不超过0.005的前提下认为玩手机对学习有影响；

    （3）现从不玩手机，学习成绩优秀的8名学生中任意选取两人，对他们的学习情况进行全程跟踪，记甲、乙两名学生被抽到的人数为X，求X的分布列和数学期望．

    附：

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥中，底面为矩形， 面， 为的中点。

    （1）证明： 平面;

    （2）设， ，三棱锥的体积 ，求A到平面PBC的距离。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，水平的广场上有一盏路灯挂在高的电线杆顶上，记电线杆的底部为点.把路灯看作一个点光源，身高的女孩站在离点的点处，回答下面的问题.

    （1）若女孩以为半径绕着电线杆走一个圆圈，人影扫过的是什么图形，求这个图形的面积；

    （2）若女孩向点前行到达点，然后从点出发沿着以为对角线的正方形走一圈，画出女孩走一圈时头顶影子的轨迹，说明轨迹的形状.

    查看答案和解析>>

    同步练习册答案