
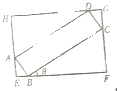
 如图,矩形ABCD的长AB=a,宽AD=b,外接矩形EFGH的面积为S,设∠CBF=θ.
如图,矩形ABCD的长AB=a,宽AD=b,外接矩形EFGH的面积为S,设∠CBF=θ.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |


科目:高中数学 来源: 题型:
 工艺扇面是中国书画一种常见的表现形式.某班级想用布料制作一面如图所示的扇面.已知扇面展开的中心角为120°,外圆半径为50cm,内圆半径为20cm.则制作这样一面扇面需要的布料为
工艺扇面是中国书画一种常见的表现形式.某班级想用布料制作一面如图所示的扇面.已知扇面展开的中心角为120°,外圆半径为50cm,内圆半径为20cm.则制作这样一面扇面需要的布料为查看答案和解析>>
科目:高中数学 来源: 题型:
| m |
| n |
| π |
| 2 |
| π |
| 2 |
| m |
| n |
| 6 |
| 5 |
| n |
| ||
| 5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com